
【題目】如圖,Rt△ABC中,AC=BC=2,正方形CDEF的頂點D,F分別在AC,BC邊上,設CD的長度為x,△ABC與正方形CDEF重疊部分的面積為y,則下列圖象中能表示y與x之間的函數關系的是( ) 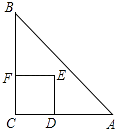
A.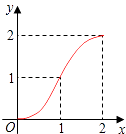
B.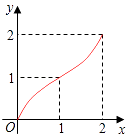
C.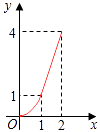
D.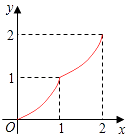
【答案】A
【解析】解:當0<x≤1時,y=x2 ,
當1<x≤2時,ED交AB于M,EF交AB于N,如圖,
CD=x,則AD=2﹣x,
∵Rt△ABC中,AC=BC=2,
∴△ADM為等腰直角三角形,
∴DM=2﹣x,
∴EM=x﹣(2﹣x)=2x﹣2,
∴S△ENM= ![]() (2x﹣2)2=2(x﹣1)2 ,
(2x﹣2)2=2(x﹣1)2 ,
∴y=x2﹣2(x﹣1)2=﹣x2+4x﹣2=﹣(x﹣2)2+2,
∴y= ![]() ,
,
故選:A.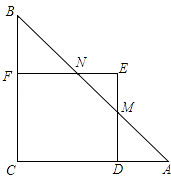
分類討論:當0<x≤1時,根據正方形的面積公式得到y=x2;當1<x≤2時,ED交AB于M,EF交AB于N,利用重疊的面積等于正方形的面積減去等腰直角三角形MNE的面積得到y=x2﹣2(x﹣1)2 , 配方得到y=﹣(x﹣2)2+2,然后根據二次函數的性質對各選項進行判斷.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:
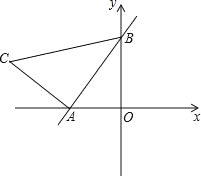
【題目】如圖,直線y=kx+2與x軸、y軸分別交于A、B兩點,OA:OB=![]() .以線段AB為邊在第二象限內作等腰Rt△ABC,∠BAC=90°.
.以線段AB為邊在第二象限內作等腰Rt△ABC,∠BAC=90°.
(1)求點A的坐標和k的值;
(2)求點C坐標;
(3)直線y=![]() x在第一象限內的圖象上是否存在點P,使得△ABP的面積與△ABC的面積相等?如果存在,求出點P坐標;如果不存在,請說明理由.
x在第一象限內的圖象上是否存在點P,使得△ABP的面積與△ABC的面積相等?如果存在,求出點P坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1的長方形ABCD中,E點在AD上,且BE=2AE.今分別以BE、CE為折線,將A、D向BC的方向折過去,圖2為對折后A、B、C、D、E五點均在同一平面上的位置圖.若圖2中,∠AED=15°,則∠BCE的度數為何?( )
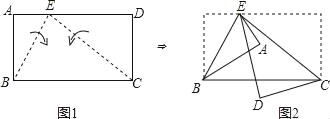
A. 30 B. 32.5 C. 35 D. 37.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將在Rt△ABC繞其銳角頂點A旋轉90°得到在Rt△ADE,連接BE,延長DE、BC相交于點F,則有∠BFE=90°,且四邊形ACFD是一個正方形.
(1)判斷△ABE的形狀,并證明你的結論;
(2)用含b代數式表示四邊形ABFE的面積;
(3)求證:a2+b2=c2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】食品安全是關乎民生的重要問題,在食品中添加過量的添加劑對人體健康有害,但適量的添加劑對人體健康無害而且有利于食品的儲存和運輸.為提高質量,做進一步研究,某飲料加工廠需生產A,B兩種飲料共100瓶,需加入同種添加劑270克,其中A飲料每瓶需加添加劑2克,B飲料每瓶需加添加劑3克,飲料加工廠生產了A,B兩種飲料各多少瓶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C是⊙O上一點,過點C的直線交AB的延長線于點D,AE⊥DC,垂足為E,F是AE與⊙O的交點,AC平分∠BAE. 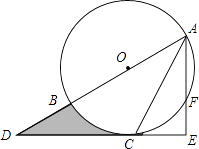
(1)求證:DE是⊙O的切線;
(2)若AE=6,∠D=30°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
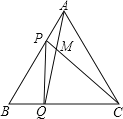
【題目】點P、Q分別是邊長為4cm的等邊![]() 的邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都是
的邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都是![]() ,設運動時間為t秒.
,設運動時間為t秒.
![]() 連接AQ、CP交于點M,則在P、Q運動的過程中,
連接AQ、CP交于點M,則在P、Q運動的過程中,![]() 變化嗎:若變化,則說明理由,若不變,則求出它的度數;
變化嗎:若變化,則說明理由,若不變,則求出它的度數;
![]() 連接PQ,
連接PQ,
![]() 當
當![]() 秒時,判斷
秒時,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
![]() 當
當![]() 時,則
時,則![]() ______秒
______秒![]() 直接寫出結果
直接寫出結果![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,有![]() 張寫有實數的卡片,它們的背面都相同,現將它們背面朝上洗勻后如圖②擺放,從中任意翻開兩張都是無理數的概率是( )
張寫有實數的卡片,它們的背面都相同,現將它們背面朝上洗勻后如圖②擺放,從中任意翻開兩張都是無理數的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com