
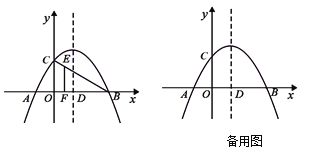
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)![]() 的圖像與x軸交于點A
的圖像與x軸交于點A![]() ,B
,B![]() ,與y軸交于點C,其對稱軸與x軸交于點D.
,與y軸交于點C,其對稱軸與x軸交于點D.
(1)求二次函數(shù)的解析式及其對稱軸;
(2)若點E是線段BC上的一點,過點E作x軸的垂線,垂足為F,且EF=2EC,求點E的坐標(biāo);
(3)若點P是拋物線對稱軸上的一個動點,連接PA,PC,設(shè)點P的縱坐標(biāo)為t,當(dāng)∠APC不小于60°時,求t的取值范圍.
【答案】(1)![]() ,對稱軸為:直線
,對稱軸為:直線![]() ;(2)
;(2)![]() ;(3)0≤t≤2.
;(3)0≤t≤2.
【解析】
(1)將A,B兩點坐標(biāo)代入到二次函數(shù)解析式中進(jìn)行求解;
(2)有多種方法進(jìn)行求解,如根據(jù)△BFF∽△BCO,求出EF的長度,即求出E點縱坐標(biāo),將E點縱坐標(biāo)代入到BC直線解析式后,求出其橫坐標(biāo)即可得到E點坐標(biāo).
(3)引入圓,分點圓上,內(nèi),外進(jìn)行分析.
(1)將A(![]() ,0),B(
,0),B(![]() ,0)代入
,0)代入![]() 得
得
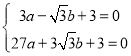
解得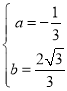 ,∴
,∴![]()
對稱軸為:直線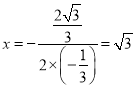 .
.
(2)如圖所示.
∵CO⊥x軸,EF⊥x軸,
∴CO//EF.
∴△BEF∽△BCO.
∴![]() .
.
設(shè)EC=m,則EF=2m.
由B(![]() ,0),C(0,3)得BC=
,0),C(0,3)得BC=![]() .
.
∴![]() .
.
解得![]() .
.
∴![]() .
.
又由![]() 得
得![]() ,∴OF=
,∴OF=![]() =
=![]() .
.
∴![]()
解法二:由B(![]() ,0),C(0,3)得BC=
,0),C(0,3)得BC=![]() ,∴∠OBC=30,
,∴∠OBC=30,
設(shè)EC=m,則EF=2m,EB=6-m.
∴![]() ,解得
,解得![]()
![]() .
.
∴![]()
![]() .
.
利用三角函數(shù)求得BF=EF÷tan 30°=![]() ,∴OF=
,∴OF=![]()
![]() =
=![]()
∴![]()
解法三:求出![]() 后,即E點的縱坐標(biāo)為
后,即E點的縱坐標(biāo)為![]() ,
,
由B(![]() ,0),C(0,3)得直線BC解析式為
,0),C(0,3)得直線BC解析式為![]() ,
,
將yE=![]() 代入
代入![]() 得xE=
得xE=![]() ,∴
,∴![]() (解法二、解法三參考解法一相應(yīng)步驟給分)
(解法二、解法三參考解法一相應(yīng)步驟給分)
(3)如圖2,由題意知∠CAO=60
作∠CAO的平分線AQ,交y軸于Q
則∠QAC=∠QCA=30
∴∠AQC=120
以Q為圓心,QA為半徑作圓,與拋物線對稱軸交于點M1,M2
當(dāng)點M在圓上時,則∠AM1C=∠AM2C=![]() ∠AQC=60.
∠AQC=60.
當(dāng)點M在圓內(nèi)時,∠AMC>60,
當(dāng)點M在圓外時,∠AMC<60,
過Q作QH垂直于對稱軸.在Rt△AOQ中,求得AQ=2,
在Rt△M1QH中,M1H=![]()
∴M1D=1+1=2,M2D=1-1=0
∴0≤t≤2.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線y=﹣x+4與x軸交于點B,與y軸交于點C,拋物線y=﹣x2+bx+c經(jīng)過B,C兩點,與x軸另一交點為A.點P以每秒![]() 個單位長度的速度在線段BC上由點B向點C運(yùn)動(點P不與點B和點C重合),設(shè)運(yùn)動時間為t秒,過點P作x軸垂線交x軸于點E,交拋物線于點M.
個單位長度的速度在線段BC上由點B向點C運(yùn)動(點P不與點B和點C重合),設(shè)運(yùn)動時間為t秒,過點P作x軸垂線交x軸于點E,交拋物線于點M.
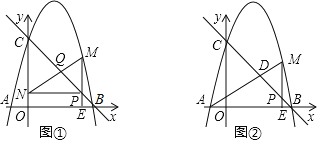
(1)求拋物線的解析式;
(2)如圖①,過點P作y軸垂線交y軸于點N,連接MN交BC于點Q,當(dāng)![]() 時,求t的值;
時,求t的值;
(3)如圖②,連接AM交BC于點D,當(dāng)△PDM是等腰三角形時,直接寫出t的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】因“抗擊疫情”需要,學(xué)校決定再次購進(jìn)一批醫(yī)用一次性口罩及KN95口罩共1000只,已知1只醫(yī)用一次性口罩和10只KN95口罩共需113元;3只醫(yī)用一次性口罩和5只KN95口罩共需64元.問:
(1)一只醫(yī)用一次性口罩和一只KN95口罩的售價分別是多少元?
(2)參照上次購買獲得的需求情況后,校長給出了一條建議:醫(yī)用一次性口罩的購買量不能多于KN95口罩?jǐn)?shù)量的2倍,請你遵循校長建議給出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,將△ABC進(jìn)行位似變換得到△A1B1C1.
(1)△ABC與△A1B1C1的位似比是 .
(2)畫出△ABC繞點O逆時針旋轉(zhuǎn)180°得到的△A2B2C2.
(3)若點P(a,b)為△ABC內(nèi)一點,求點P在△A2B2C2內(nèi)的對應(yīng)點P2的坐標(biāo).
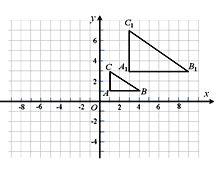
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】中華文明,源遠(yuǎn)流長;中華漢字,寓意深廣.為了傳承中華民族優(yōu)秀傳統(tǒng)文化,我市某中學(xué)舉行“漢字聽寫”比賽,賽后整理參賽學(xué)生的成績,將學(xué)生的成績分為A,B,C,D四個等級,并將結(jié)果繪制成如圖所示的條形統(tǒng)計圖和扇形統(tǒng)計圖,但均不完整.

請你根據(jù)統(tǒng)計圖解答下列問題:
(1)參加比賽的學(xué)生共有____名;
(2)在扇形統(tǒng)計圖中,m的值為____,表示“D等級”的扇形的圓心角為____度;
(3)組委會決定從本次比賽獲得A等級的學(xué)生中,選出2名去參加全市中學(xué)生“漢字聽寫”大賽.已知A等級學(xué)生中男生有1名,請用列表法或畫樹狀圖法求出所選2名學(xué)生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,直線![]() 與雙曲線
與雙曲線![]() 相交于點
相交于點![]() .
.
![]() 求雙曲線
求雙曲線![]() 的表達(dá)式;
的表達(dá)式;
![]() 過動點
過動點![]() 且垂直于x軸的直線與直線
且垂直于x軸的直線與直線![]() 及雙曲線
及雙曲線![]() 的交點分別為B和C,當(dāng)點B位于點C下方時,求出n的取值范圍.
的交點分別為B和C,當(dāng)點B位于點C下方時,求出n的取值范圍.
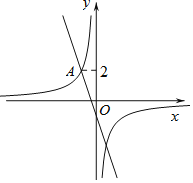
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 中,D、E分別在AB、AC上,下列條件中,能推斷
中,D、E分別在AB、AC上,下列條件中,能推斷![]() 與
與![]() 相似的有( )個
相似的有( )個
①∠BDE+∠C=180°;②![]() ;③
;③![]() ;④∠A=90°,且
;④∠A=90°,且![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,半徑為5的⊙A中,弦BC,ED所對的圓心角分別是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,則弦BC的弦心距等于 .
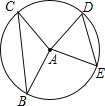
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com