
【題目】如圖,拋物線y=ax2+bx﹣1(a≠0)經過A(﹣1,0),B(2,0)兩點,與y軸交于點C.
(1)求拋物線的解析式及頂點D的坐標;
(2)點P在拋物線的對稱軸上,當△ACP的周長最小時,求出點P的坐標;
(3)點N在拋物線上,點M在拋物線的對稱軸上,是否存在以點N為直角頂點的Rt△DNM與Rt△BOC相似?若存在,請求出所有符合條件的點N的坐標;若不存在,請說明理由.
【答案】
(1)
解:∵拋物線y=ax2+bx﹣1(a≠0)經過A(﹣1,0),B(2,0)兩點,
∴ ![]()
∴  ,
,
∴拋物線解析式為y= ![]() x2﹣
x2﹣ ![]() x﹣1=
x﹣1= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴拋物線的頂點坐標為( ![]() ,﹣
,﹣ ![]() )
)
(2)
解:如圖1,

連接BC與拋物線對稱軸的交點就是點P,連接AC,AP,
∵點A,B關于拋物線對稱軸對稱,
∴PA=PB,
∵B(2,0),C(0,﹣1),
∴直線BC解析式為y= ![]() x﹣1,
x﹣1,
∵點P在拋物線對稱軸上,
∴點P的橫坐標為 ![]() ,
,
∴點P的縱坐標為﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:如圖2,

過點作NF⊥DM,
∵B(2,0),C(0,﹣1),
∴OB=2,OC=1,
∴tan∠OBC= ![]() =
= ![]() ,tan∠OCB=
,tan∠OCB= ![]() =2,
=2,
設點N(m, ![]() m2﹣
m2﹣ ![]() m﹣1),
m﹣1),
∴FN=|m﹣ ![]() |,FD=|
|,FD=| ![]() m2﹣
m2﹣ ![]() m﹣1+
m﹣1+ ![]() |=|
|=| ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() |,
|,
∵Rt△DNM與Rt△BOC相似,
∴∠MDN=∠OBC,或∠MDN=∠OCB,
①當∠MDN=∠OBC時,
∴tan∠MDN= ![]() =
= ![]() ,
,
∴ 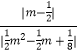 =
= ![]()
∴m= ![]() (舍)或m=
(舍)或m= ![]() 或m=﹣
或m=﹣ ![]() ,
,
∴N( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ),
),
②當∠MDN=∠OCB時,
∴tan∠MDN= ![]() =2,
=2,
∴ 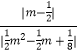 =2,
=2,
∴m= ![]() (舍)或m=
(舍)或m= ![]() 或m=﹣
或m=﹣ ![]() ,
,
∴N( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() );
);
∴符合條件的點N的坐標( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)利用待定系數法求出拋物線解析式;(2)確定出當△ACP的周長最小時,點P就是BC和對稱軸的交點,利用兩點間的距離公式計算即可?(3)作出輔助線,利用tan∠MDN=2或 ![]() ,建立關于點N的橫坐標的方程,求出即可.此題是二次函數綜合題,主要考查了待定系數法,拋物線的對稱性,三角函數,三角形周長的計算,絕對值方程,過點N作拋物線對稱軸的垂線是解本題的關鍵也是難點.
,建立關于點N的橫坐標的方程,求出即可.此題是二次函數綜合題,主要考查了待定系數法,拋物線的對稱性,三角函數,三角形周長的計算,絕對值方程,過點N作拋物線對稱軸的垂線是解本題的關鍵也是難點.
【考點精析】本題主要考查了二次函數圖象的平移和解直角三角形的相關知識點,需要掌握平移步驟:(1)配方 y=a(x-h)2+k,確定頂點(h,k)(2)對x軸左加右減;對y軸上加下減;解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法)才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=30°,P是∠AOB平分線上一點,CP∥OB,交OA于點C,PD⊥OB,垂足為點D,且PC=4,則PD等于( ) 
A.1
B.2
C.4
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究
問題1 已知:如圖1,三角形ABC中,點D是AB邊的中點,AE⊥BC,BF⊥AC,垂足分別為點E,F,AE,BF交于點M,連接DE,DF.若DE=kDF,則k的值為 .
拓展
問題2 已知:如圖2,三角形ABC中,CB=CA,點D是AB邊的中點,點M在三角形ABC的內部,且∠MAC=∠MBC,過點M分別作ME⊥BC,MF⊥AC,垂足分別為點E,F,連接DE,DF.求證:DE=DF.
推廣
問題3 如圖3,若將上面問題2中的條件“CB=CA”變為“CB≠CA”,其他條件不變,試探究DE與DF之間的數量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,小明購買一種筆記本所付款金額y(元)與購買量x(本)之間的函數圖象由線段OB和射線BE組成,則一次購買8個筆記本比分8次購買每次購買1個可節省元. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年黔西南州教育局組織全州中小學生參加全省安全知識網絡競賽,在全州安全知識競賽結束后,通過網上查詢,某校一名班主任對本班成績(成績取整數,滿分100分)作了統計分析,繪制成如下頻數分布表和頻數分布直方圖,請你根據圖表提供的信息,解答下列問題: 
(1)頻數分布表中a= , b= , c=
(2)補全頻數分布直方圖
(3)為了激勵學生增強安全意識,班主任準備從超過90分的學生中選2人介紹學習經驗,那么取得100分的小亮和小華同時被選上的概率是多少?請用列表法或畫樹狀圖加以說明,并列出所有等可能結果.
頻數分布表
分組(分) | 頻數 | 頻率 |
50<x 60 | 2 | 0.04 |
60<x 70 | 12 | a |
70<x<80 | b | 0.36 |
80<x 90 | 14 | 0.28 |
90<x 100 | c | 0.08 |
合計 | 50 | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線n與過原點的直線m交于點P,P點的坐標如圖所示,直線n與y軸交于點A;若OA=OP;
(1)求A點的坐標;
(2)求直線m,n的函數表達式;
(3)求△AOP的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com