
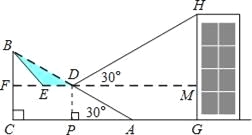
【題目】如圖,已知斜坡AB長為80米,坡角(即∠BAC)為30°,BC⊥AC,現計劃在斜坡中點D處挖去部分坡體(用陰影表示)修建一個平行于水平線CA的平臺DE和一條新的斜坡BE.
(1)若修建的斜坡BE的坡角為45°,求平臺DE的長;(結果保留根號)
(2)一座建筑物GH距離A處36米遠(即AG為36米),小明在D處測得建筑物頂部H的仰角(即∠HDM)為30°.點B、C、A、G、H在同一個平面內,點C、A、G在同一條直線上,且HG⊥CG,求建筑物GH的高度.(結果保留根號)

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據題意得出∠BEF=45°,解直角△BDF,求出BF,DF,進而得出EF的長,即可得出答案;
(2)利用在Rt△DPA中,DP=![]() AD,以及PA=ADcos30°進而得出DM的長,利用HM=DMtan30°得出即可.
AD,以及PA=ADcos30°進而得出DM的長,利用HM=DMtan30°得出即可.
試題解析:(1)∵修建的斜坡BE的坡角為45°,
∴∠BEF=45°,
∵∠DAC=∠BDF=30°,AD=BD=40,
∴BF=EF=![]() BD=20,DF=20
BD=20,DF=20![]() ,
,
∴DE=DF﹣EF=20![]() ﹣20,
﹣20,
∴平臺DE的長為(20![]() ﹣20)米;
﹣20)米;
(2)過點D作DP⊥AC,垂足為P.
在Rt△DPA中,DP=![]() AD=
AD=![]() ×40=20,PA=ADcos30°=20
×40=20,PA=ADcos30°=20![]() ,
,
在矩形DPGM中,MG=DP=20,DM=PG=PA+AG=20![]() +36.
+36.
在Rt△DMH中,HM=DMtan30°=(20![]() +36)×
+36)×![]() =20+12
=20+12![]() ,
,
則GH=HM+MG=20+12![]() +20=40+12
+20=40+12![]() .
.
答:建筑物GH高為(40+12![]() )米.
)米.


科目:初中數學 來源: 題型:
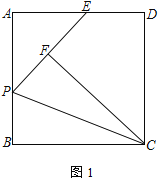
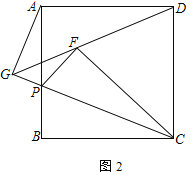
【題目】如圖,正方形ABCD中,點P為AB邊上一點,將△BCP沿CP翻折至△FCP位置,延長至PF交邊AD于E點.
(1) 求證:EF=DE.
(2) 若DF延長線與CP延長線交于G點,求![]() 的值.
的值.
(3) 在(2)的條件下,若正方形的邊長為![]() ,
, ![]() ,直接寫出DG的長為___________.
,直接寫出DG的長為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
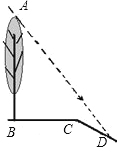
【題目】如圖,坡面CD的坡比為![]() ,坡頂的平地BC上有一棵小樹AB,當太陽光線與水平線夾角成60°時,測得小樹的在坡頂平地上的樹影BC是3米,斜坡上的樹影CD是
,坡頂的平地BC上有一棵小樹AB,當太陽光線與水平線夾角成60°時,測得小樹的在坡頂平地上的樹影BC是3米,斜坡上的樹影CD是![]() 米,則小樹AB的高是 米.
米,則小樹AB的高是 米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聯合國規定每年的6月5日是“世界環境日”,為配合今年的“世界環境日”宣傳活動,某校課外活動小組對全校師生開展了以“愛護環境,從我做起”為主題的問卷調查活動,將調查結果分析整理后,制成了上面的兩個統計圖.
其中:A:能將垃圾放到規定的地方,而且還會考慮垃圾的分類;
B:能將垃圾放到規定的地方,但不會考慮垃圾的分類;
C:偶爾會將垃圾放到規定的地方;
D:隨手亂扔垃圾.
根據以上信息回答下列問題:
(1)該校課外活動小組共調查了多少人?并補全上面的條形統計圖;
(2)如果該校共有師生2400人,那么隨手亂扔垃圾的約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=∠90°,D為AB邊上一點. 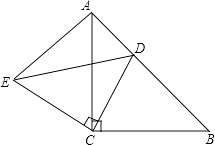
(1)求證:△ACE≌△BCD;
(2)若AD=6,BD=8,求ED的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩同學的家與學校的距離均為3000米.甲同學先步行600米,然后乘公交車去學校、乙同學騎自行車去學校.已知甲步行速度是乙騎自行車速度的![]() ,公交車的速度是乙騎自行車速度的2倍.甲乙兩同學同時從家發去學校,結果甲同學比乙同學早到2分鐘.
,公交車的速度是乙騎自行車速度的2倍.甲乙兩同學同時從家發去學校,結果甲同學比乙同學早到2分鐘.
(1)求乙騎自行車的速度;
(2)當甲到達學校時,乙同學離學校還有多遠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com