【題目】已知點（2，-4）在正比例函數y=kx的圖象上。
（1）求k的值；
（2）若點（-1，m）在函數y=kx的圖象上，試求出m的值；
（3）若A（
，y1），B（-2，y2），C（1，y3）都在此函數圖象上，試比較y1，y2，y3的大小。
【答案】（1）k=-2.（2）m=2.（3）y3<y1<y2
【解析】試題分析：（1）把點（2，-4）代入函數y=kx，即可求得k的值；（2）再把點（-1，m）代入函數解析式即可求得m的值；（3）利用正比例函數的增減性，比較三個的橫坐標的大小，即可求得y1、y2、y3的大小.
解：（1）把點（2，-4）的坐標代入正比例函數y=kx得-4=2k，解得k=-2.
（2）把點（-1，m）的坐標代入y=-2x得m=2.
（3）方法1：因為函數y=-2x中，y隨x的增大而減小，-2<
<1，所以y3<y1<y2.
方法2：y1=（-2）×=-1，y2=（-2）×（-2）=4，y3=（-2）×1=-2，所以y3<y1<y2.
仁愛英語同步練習冊系列答案
學習實踐園地系列答案科目：初中數學 來源： 題型：
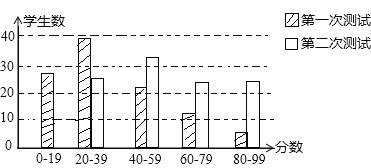
【題目】有100名學生參加兩次科技知識測試，條形圖顯示兩次測試的分數分布情況．
請你根據條形圖提供的信息，回答下列問題（把答案填在題中橫線上）：
（1）兩次測試最低分在第 次測試中；
（2）第 次測試成績較好；
（3）第一次測試中，中位數在 分數段，第二次測試中，中位數在 分數段．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是平行四邊形．
（1）利用尺規作∠ABC的平分線BE，交AD于E（保留作圖痕跡，不寫作法）；
（2）在（1）所作的圖形中，求證：AB=AE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知一次函數y=kx+b（k≠0）的圖象與x軸、y軸分別交于A、B兩點，且與反比例函數y=
（m≠0）的圖象在第一象限交于點C，CD垂直于x軸，垂足為D，若OA=OB=OD=1．
（1）求點A、B、D的坐標；
（2）求一次函數與反比例函數的解析式；
（3）在x＞0的條件下，根據圖象說出反比例函數的值大于一次函數值的x的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com