Question

【題目】如圖，已知等邊和等邊，點在的延長線上，的延長線交于點M，連，若，則（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

根據等腰三角形的性質得到AB=BC，∠ABP=∠CBE=60°，PB=PE，證得△APB≌△CEB （SAS），根據全等三角形的性質得到∠APB=∠CEB，于是得到∠PME=∠PBE=60゜，作BN⊥AM于N，BF⊥ME于F，通過△BNP≌△BFE（AAS），得到BN=BF，根據角平分線的性質得到BM平分∠AME，求得∠AMB=∠AME=×120°=60°，根據三角形的內角和即可得到結論．

∵等邊△ABC和等邊△BPE，

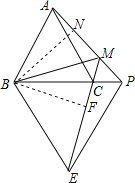
∴AB=BC，∠ABP=∠CBE=60°，PB=PE，
在△APB和△CEB中，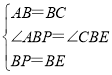
，
∴△APB≌△CEB （SAS），
∴∠APB=∠CEB，
∵∠MCP=∠BCE，
∴∠PME=∠PBE=60゜，
作BN⊥AM于N，BF⊥ME于F，
∵△APB≌△CEB，
∴BP=BE，∠BPN=∠FEB，
在△BNP和△BFE中，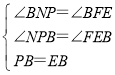
，
∴△BNP≌△BFE（AAS），
∴BN=BF，
∴BM平分∠AME，
∴∠AMB=∠AME=×120°=60°，
∵∠ABM=40°，
∴∠BAP=80°，
∴∠APB=180°-∠ABP-∠BAP=40°．
故選：A．