
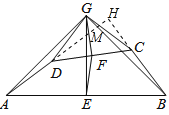
【題目】如下圖1,在四邊形ABCD中,點E、F分別是AB、CD的中點.過點E作AB的垂線,過點F作CD的垂線,兩垂線交于點G,連結GA、GB、GC、GD、EF,若∠AGD=∠BGC.

(1)求證:AD=BC;
(2)求證:△AGD∽△EGF;
(3)如圖2,若AD、BC所在直線互相垂直,求![]() 的值.
的值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
試題分析:本題是相似形綜合題目,考查了線段垂直平分線的性質、全等三角形的判定與性質、相似三角形的判定與性質、三角函數等知識;本題難度較大,綜合性強,特別是(3)中,需要通過作輔助線綜合運用(1)(2)的結論和三角函數才能得出結果.
(2)先證出∠AGB=∠DGC,由![]() =
=![]() ,證出△AGB∽△DGC,得出比例式
,證出△AGB∽△DGC,得出比例式![]() =
=![]() ,再證出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再證出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延長AD交GB于點M,交BC的延長線于點H,則AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGE=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() =
=![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值即可.
的值即可.
試題解析:(1)∵GE是AB的垂直平分線,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
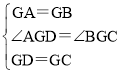 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中,![]() =
=![]() ,
,
∴△AGB∽△DGC,
∴![]() =
=![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延長AD交GB于點M,交BC的延長線于點H,如圖所示,則AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() =
=![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() =
=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A. 正比例函數是一次函數的特殊形式B. 一次函數不一定是正比例函數
C. y=kx+b是一次函數D. 2x-y=0是正比例函數
查看答案和解析>>
科目:初中數學 來源: 題型:
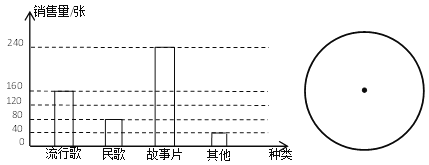
【題目】小明對某音像制品店十月份的銷售量情況進行調查.如圖是小明對所調查結果的條形統計圖.
(1)該店十月份共銷售多少張音像制品?
(2)請你改用扇形統計圖來表示該店十月份銷售音像制品的種類.
(3)從統計圖中看,流行歌類與民歌類銷售量之比是多少?故事片占總銷售量的百分比是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知四邊形ABCD為菱形,且A(0,3)、B(-4,0).
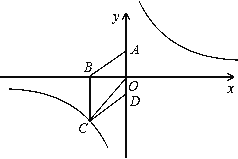
(1)求經過點C的反比例函數的解析式;
(2)設P是(1)中所求函數圖象上一點,以P、O、A頂點的三角形的面積與△COD的面積相等.求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在圓柱、正方體、長方體中,主視圖可能一樣的是 ( )
A. 僅圓柱和正方體 B. 僅圓柱和長方體
C. 僅正方體和長方體 D. 圓柱、正方體和長方體
查看答案和解析>>
科目:初中數學 來源: 題型:
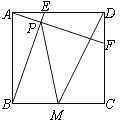
【題目】如圖,正方形ABCD中,AB=4,動點E從點A出發向點D運動,同時動點F從點D出發向點C運動,點E、F運動的速度相同,當它們到達各自終點時停止運動,運動過程中線段AF、BE相交于點P,M是線段BC上任意一點,則MD+MP的最小值為.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com