
���}Ŀ������ABC�У���ACB��90����AC��BC��ֱ��,MN��(j��ng)�^(gu��)�c(di��n)C����AD��MN���c(di��n)D��BE��MN���c(di��n)E��

��1����(d��ng)ֱ��MN�@�c(di��n)C���D(zhu��n)����D1��λ�Õr(sh��)�����C��DE=AD+BE��
��2����(d��ng)ֱ��MN�@�c(di��n)C���D(zhu��n)����D2��λ�Õr(sh��)�����C��DE��AD��BE��
��3����(d��ng)ֱ��MN�@�c(di��n)C���D(zhu��n)����D3��λ�Õr(sh��)������DE��AD��BE֮�g����ʲô�ӵĔ�(sh��)���P(gu��n)ϵ��Ո(q��ng)�㌑���@��(g��)��(sh��)���P(gu��n)ϵ�����C��
���𰸡���1���C��Ҋ(ji��n)Ԕ�⣻��2���C��Ҋ(ji��n)Ԕ�⣻��3��DE=BE-AD������Ҋ(ji��n)Ԕ��.
��������
��1�����ô�ֱ�Ķ��x�á�ADC=��CEB=90�㣬�t����(j��)����á�DAC+��ACD=90�㣬�ٸ���(j��)�Ƚǵ������ȵõ���DAC=��BCE��Ȼ�����(j��)��AAS�����Д��ADC�ա�CEB������CD=BE��AD=CE�������õ������Q�õ�DE=AD+BE��
��2���c��1��һ�ӿ��C����ADC�ա�CEB���tCD=BE��AD=CE��������DE=CE-CD=AD-BE��
��3���c��1��һ�ӿ��C����ADC�ա�CEB���tCD=BE��AD=CE��������DE=CD-CE=BE-AD��
��1���C������AD��MN��BE��MN��
���ADC=��CEB=90�㣬
���DAC+��ACD=90�㣬
�ߡ�ACB=90�㣬
���BCE+��ACD=90�㣬
���DAC=��BCE��
�ڡ�ADC�͡�CEB��
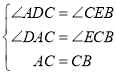 ��
��
���ADC�ա�CEB��AAS����
��CD=BE��AD=CE��
��DE=CE+CD=AD+BE��
��2���C�����c��1��ͬ�������C����ADC�ա�CEB��
��CD=BE��AD=CE��
��DE=CE-CD=AD-BE��
��3��DE=BE-AD
�C�����c��1��ͬ�������C����ADC�ա�CEB��
��CD=BE��AD=CE��
��DE=CD-CE=BE-AD��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ����![]() �У�
�У�![]() �քe��
�քe��![]() �����c(di��n)��
�����c(di��n)��![]() �քe��
�քe��![]() ���c(di��n)
���c(di��n)![]() .�������}����_����
.�������}����_����

A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У���BAC=45�㣬��BD=2��CD=3��AD��BC��D������ABD��AB���ڵ�ֱ���ۯB��ʹ�c(di��n)D�����c(di��n)E̎������ACD��AC���ڵ�ֱ���ۯB��ʹ�c(di��n)D�����c(di��n)F̎���քe���L(zh��ng)EB��FCʹ�佻���c(di��n)M��
(1)�Д���߅��AEMF���Π���o���C����
(2)�O(sh��)AD=x�����ù��ɶ����������P(gu��n)��x�ķ���ģ�ͣ�����߅��AEMF����e.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() �;���
�;���![]() ��
��

��1����Ҫ�����D(�����������E����������)��
���L(zh��ng)����![]() ���c(di��n)
���c(di��n)![]() ��ʹ
��ʹ![]() ���������L(zh��ng)����
���������L(zh��ng)����![]() ���c(di��n)
���c(di��n)![]() ��ʹ
��ʹ![]() ��
��
��2�����![]() ��
��![]() �քe�Ǿ���
�քe�Ǿ���![]() ��
��![]() �����c(di��n)����
�����c(di��n)����![]() ��
��![]() ����
����![]() ���L(zh��ng)��
���L(zh��ng)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij܇�g�ӵ�һ�����ڣ�������ǰ����ɵ�����ӹ��΄�(w��)�����ÿ��ӹ�150��(g��)���tǡ�ð�����ɣ����ÿ��ӹ�200��(g��)���t�ɱ�ԭӋ(j��)����ǰ5����ɣ�
��1�����@�������(g��)��(sh��)��
��2��܇�g��ÿ��ӹ�200��(g��)������ٶȼӹ���![]() ��(g��)���������˼ӹ��ٶȣ�ÿ��ӹ�250��(g��)������Y(ji��)����ԭӋ(j��)����ǰ6����������a(ch��n)�΄�(w��)����
��(g��)���������˼ӹ��ٶȣ�ÿ��ӹ�250��(g��)������Y(ji��)����ԭӋ(j��)����ǰ6����������a(ch��n)�΄�(w��)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ�κ���(sh��)�D��(j��ng)�^(gu��)�c(di��n)(4,-1)�����cֱ��![]() ƽ�У���һ�κ���(sh��)����ʽ���@��(g��)����(sh��)�D���c������(bi��o)�S���ɵ������ε���e.
ƽ�У���һ�κ���(sh��)����ʽ���@��(g��)����(sh��)�D���c������(bi��o)�S���ɵ������ε���e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����Gˮ��ɽ���ǽ�ɽ�yɽ�����鱣�o(h��)���B(t��i)�h(hu��n)����A��B�ɴ��(zh��n)������������م^(q��)���B(y��ng)�~�W(w��ng)��Ͳ��~�W(w��ng)�䣬ÿ�兢�������˔�(sh��)�����_֧���±���

��1����ɴ�����ͬO�ߵ��˾�֧���M(f��i)��һ�ӣ��������B(y��ng)�~�W(w��ng)��Ͳ��~�W(w��ng)����˾�֧���M(f��i)�ø��Ƕ���Ԫ��
��2�����˾�֧���M(f��i)�ò�׃����r�£��鹝(ji��)�s�_֧���ɴ��(zh��n)��f(xi��)�{(di��o)40�˹�ͬ�����B(y��ng)�~�W(w��ng)��Ͳ��~�W(w��ng)�䣮Ҫʹ��֧�������^(gu��)102000Ԫ���������B(y��ng)�~�W(w��ng)���˔�(sh��)С���������~�W(w��ng)���˔�(sh��)���t���ĎN���������ˆT������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��![]() ��(j��ng)�^(gu��)
��(j��ng)�^(gu��)![]() ��c(di��n)
��c(di��n)![]() ��һ�lֱ����
��һ�lֱ����![]() ��
��![]() �քe��ֱ��
�քe��ֱ��![]() �σ��c(di��n)����
�σ��c(di��n)����![]() ��
��
��1����ֱ��![]() ��(j��ng)�^(gu��)
��(j��ng)�^(gu��)![]() �ă�(n��i)������
�ă�(n��i)������![]() ���侀
���侀![]() �ϣ�Ո(q��ng)��Q����ɂ�(g��)��(w��n)�}��
�ϣ�Ո(q��ng)��Q����ɂ�(g��)��(w��n)�}��
����D1����![]() ��
��![]() ��
��
�t![]()
![]() ��
��![]()
![]() ������
������![]() ������
������![]() ������
������![]() ������
������
����D2����![]() ��Ո(q��ng)?zh��)���һ��(g��)�P(gu��n)��
��Ո(q��ng)?zh��)���һ��(g��)�P(gu��n)��![]() �c
�c![]() �P(gu��n)ϵ�ėl�� ��ʹ���еăɂ�(g��)�Y(ji��)Փ��Ȼ���������C���ɂ�(g��)�Y(ji��)Փ������
�P(gu��n)ϵ�ėl�� ��ʹ���еăɂ�(g��)�Y(ji��)Փ��Ȼ���������C���ɂ�(g��)�Y(ji��)Փ������
��2����D3����ֱ��![]() ��(j��ng)�^(gu��)
��(j��ng)�^(gu��)![]() ���ⲿ��
���ⲿ��![]() ��Ո(q��ng)?zh��)�?/span>
��Ո(q��ng)?zh��)�?/span>![]() ���l���Δ�(sh��)���P(gu��n)ϵ�ĺ������루��Ҫ���C������
���l���Δ�(sh��)���P(gu��n)ϵ�ĺ������루��Ҫ���C������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ�У�ֱ��![]() �քe�c
�քe�c![]() �S��
�S��![]() �S�����c(di��n)
�S�����c(di��n)![]() ��
��![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �����c(di��n).
�����c(di��n).
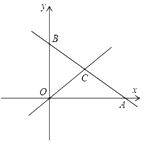
��1���c(di��n)![]() ������(bi��o)��________���c(di��n)
������(bi��o)��________���c(di��n)![]() ������(bi��o)��________;
������(bi��o)��________;
��2��ֱ��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ����
����![]() ��ԇ����c(di��n)
��ԇ����c(di��n)![]() ������(bi��o)��
������(bi��o)��
��3�����c(di��n)![]() ��ֱ��
��ֱ��![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)�c(di��n)
�ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)�c(di��n)![]() ��
��![]() �S�Ĵ������cֱ��
�S�Ĵ������cֱ��![]() �����c(di��n)
�����c(di��n)![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ������
������![]() ���L(zh��ng)�Ȟ�
���L(zh��ng)�Ȟ�![]() ����
����![]() �c
�c![]() �ĺ���(sh��)����ʽ.
�ĺ���(sh��)����ʽ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com