
【題目】已知:如圖所示,∠ABD和∠BDC的平分線交于E,BE交CD于點F,∠1+∠2=90°. 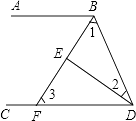
(1)求證:AB∥CD;
(2)試探究∠2與∠3的數量關系.
【答案】
(1)證明:∵BE、DE平分∠ABD、∠BDC,
∴∠1= ![]() ∠ABD,∠2=
∠ABD,∠2= ![]() ∠BDC;
∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁內角互補,兩直線平行)
(2)解:∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
【解析】(1)已知BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根據同旁內角互補,可得兩直線平行.(2)已知∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,將等角代換,即可得出∠3與∠2的數量關系.
【考點精析】關于本題考查的角的平分線和平行線的判定,需要了解從一個角的頂點引出的一條射線,把這個角分成兩個相等的角,這條射線叫做這個角的平分線;同位角相等,兩直線平行;內錯角相等,兩直線平行;同旁內角互補,兩直線平行才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
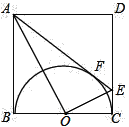
【題目】如圖,在正方形ABCD中,以BC為直徑的正方形內,作半圓O,AE切半圓于點F交CD于E
(1) 求證:AO⊥EO
(2) 連接DF,求tan∠FDE的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一個含有45°角的直角三角板的直角頂點放在一張寬為2cm的矩形紙帶邊沿上,另一個頂點在紙帶的另一邊沿上.若測得三角板的一邊與紙帶的一邊所在的直線成30°角,則三角板最長邊的長是( ) 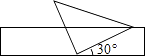
A.2cm
B.4cm
C.2 ![]() cm
cm
D.4 ![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地2014年為做好“精準扶貧”,投入資金1280萬元用于異地安置,并規劃投入資金逐年增加.2016年在2014年的基礎上增加投入資金1600萬元,從2014年到2016年,該地投入異地安置資金的年平均增長率為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y與x之間有下列關系:y=x2-1.顯然,當x=1時,y=0;當x=2時,y=3。在這個等式中( )
A. x是變量,y是常量
B. x是變量,y是常量
C. x是常量,y是變量
D. x是變量,y是變量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,BF、DE相交于點A,BG交BF于點B,交AC于點C. 
(1)指出ED、BC被BF所截的同位角,內錯角,同旁內角;
(2)指出ED、BC被AC所截的內錯角,同旁內角;
(3)指出FB、BC被AC所截的內錯角,同旁內角.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備設計一款女生校服,對全校女生喜歡的顏色進行了問卷調查,統計如下表所示:
顏色 | 黃色 | 綠色 | 白色 | 紫色 | 紅色 |
學生人數 | 100 | 180 | 220 | 80 | 750 |
學校決定采用紅色,可用來解釋這一現象的統計知識是( )
A. 平均 B. 中位數 C. 眾數 D. 方差
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com