
【題目】如圖,點O是線段AB上的點,點C,D分別是線段OA,OB的中點,小明很輕松地求得CD=![]() AB.他在反思過程中突發奇想:若點O在線段AB的延長線上或在直線AB外,則原有的結論“CD=
AB.他在反思過程中突發奇想:若點O在線段AB的延長線上或在直線AB外,則原有的結論“CD=![]() AB”仍然成立嗎?請幫小明解決此問題(當點O在線段AB的延長線上時,請畫圖分析該結論是否成立,并說明理由;當點O在直線AB外時,作出圖形,通過度量說明該結論是否成立).
AB”仍然成立嗎?請幫小明解決此問題(當點O在線段AB的延長線上時,請畫圖分析該結論是否成立,并說明理由;當點O在直線AB外時,作出圖形,通過度量說明該結論是否成立).
![]()
 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有紅、黃、白三種顏色的球共100個,它們除顏色外都相同,其中黃球的個數是白球個數的2倍少5個,已知從袋中摸出一個紅球的概率是 ![]() .
.
(1)求袋中紅球的個數;
(2)求從袋中摸出一個球是白球的概率;
(3)取走5個黃球5個白球,求從剩余的球中摸出一個球是紅球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】回答下面的例題:
解方程:x2﹣|x|﹣2=0.
解:①x≥0時,原方程化為x2﹣x﹣2=0,解得x1=2,x2=﹣1(不合題意,舍去).
②x<0時,原方程化為x2+x﹣2=0,解得x1=﹣2,x2=1(不合題意,舍去).
∴原方程的根是x1=2,x2=﹣2.
請參照例題解方程x2+|x﹣4|﹣8=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點O為坐標原點,點B的坐標為(4,3),點A、C在坐標軸上,點P在BC邊上,直線l1:y=2x+3,直線l2:y=2x﹣3.
(1)分別求直線l1與x軸,直線l2與AB的交點坐標;
(2)已知點M在第一象限,且是直線l2上的點,若△APM是等腰直角三角形,求點M的坐標;
(3)我們把直線l1和直線l2上的點所組成的圖形為圖形F.已知矩形ANPQ的頂點N在圖形F上,Q是坐標平面內的點,且N點的橫坐標為x,請直接寫出x的取值范圍(不用說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:
(1)圖1中a的值為;
(2)求統計的這組初賽成績數據的平均數、眾數和中位數;
(3)根據這組初賽成績,由高到低確定9人進入復賽,請直接寫出初賽成績為1.65m的運動員能否進入復賽.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=6,AE⊥BD,垂足為E,ED=3BE,點P、Q分別在BD,AD上,則AP+PQ的最小值為( ) 
A.2 ![]()
B.![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線l1:y=x+3與x軸交于點A,與y軸交于點B,且與雙曲線y= ![]() 交于點C(1,a).
交于點C(1,a).
(1)試確定雙曲線的函數表達式;
(2)將l1沿y軸翻折后,得到l2 , 畫出l2的圖象,并求出l2的函數表達式;
(3)在(2)的條件下,點P是線段AC上點(不包括端點),過點P作x軸的平行線,分別交l2于點M,交雙曲線于點N,求S△AMN的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E為邊CD上一點,將△ADE沿AE折疊至△AD′E處,AD′與CE交于點F.若∠B=52°,∠DAE=20°,則∠FED′的大小為 . 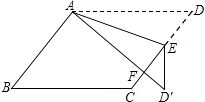
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一次數學課外實踐活動中,小聰在距離旗桿10m的A處測得旗桿頂端B的仰角為60°,測角儀高AD為1m,則旗桿高BC為 m(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com