
【題目】如圖,在數軸上,點![]() 表示
表示![]() ,點
,點![]() 表示
表示![]() ,點
,點![]() 表示
表示![]() .動點
.動點![]() 從點
從點![]() 出發,沿數軸正方向以每秒
出發,沿數軸正方向以每秒![]() 個單位的速度勻速運動;同時,動點
個單位的速度勻速運動;同時,動點![]() 從點
從點![]() 出發,沿數軸負方向以每秒
出發,沿數軸負方向以每秒![]() 個單位的速度勻速運動.設運動時間為
個單位的速度勻速運動.設運動時間為![]() 秒.
秒.
(1)當![]() 為何值時,
為何值時,![]() 、
、![]() 兩點相遇?相遇點
兩點相遇?相遇點![]() 所對應的數是多少?
所對應的數是多少?
(2)在點![]() 出發后到達點
出發后到達點![]() 之前,求
之前,求![]() 為何值時,點
為何值時,點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到點
到點![]() 的距離相等;
的距離相等;
(3)在點![]() 向右運動的過程中,
向右運動的過程中,![]() 是
是![]() 的中點,在點
的中點,在點![]() 到達點
到達點![]() 之前,求
之前,求![]() 的值.
的值.

【答案】(1)![]() ;
;![]() ;(2)3或
;(2)3或![]() ;(3)28.
;(3)28.
【解析】
(1)根據題意,由相遇時P、Q兩點的路程和為28列出方程求解即可;
(2)由題意得,t的值大于0且小于7.分點P在點O的左邊,點P在點O的右邊兩種情況討論即可求解;
(3)根據中點的定義得到AN=PN=![]() AP=t,可得CN=AC-AN=28-t,PC=28-AP=28-2t,再代入計算即可求解.
AP=t,可得CN=AC-AN=28-t,PC=28-AP=28-2t,再代入計算即可求解.
解:(1)根據題意得2t+t=28,
解得t=![]() ,
,
∴AM=![]() >10,
>10,
∴M在O的右側,且OM=![]() -10=
-10=![]() ,
,
∴當t=![]() 時,P、Q兩點相遇,相遇點M所對應的數是
時,P、Q兩點相遇,相遇點M所對應的數是![]() ;
;
(2)由題意得,t的值大于0且小于7.
若點P在點O的左邊,則10-2t=7-t,解得t=3.
若點P在點O的右邊,則2t-10=7-t,解得t=![]() .
.
綜上所述,t的值為3或![]() 時,點P到點O的距離與點Q到點B的距離相等;
時,點P到點O的距離與點Q到點B的距離相等;
(3)∵N是AP的中點,
∴AN=PN=![]() AP=t,
AP=t,
∴CN=AC-AN=28-t,PC=28-AP=28-2t,
2CN-PC=2(28-t)-(28-2t)=28.


科目:初中數學 來源: 題型:
【題目】已知A(8,0)及在第一象限的動點P(x,y),且x+y=10,設△OPA的面積為S
(1)求S關于x的函數表達式;
(2)求x的取值范圍;
(3)求S=12時P點坐標;
(4)畫出函數S的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠BOC=2∠AOC,OD平分∠AOB,∠BOE=90°,若∠AOC=40°,則∠DOE的度數等于( )
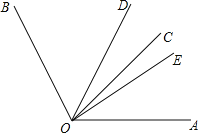
A.20°B.25°C.30°D.30°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:各類方程的解法:求解一元一次方程,根據等式的基本性質,把方程轉化為x=a的形式.求解二元一次方程組,把它轉化為一元一次方程來解;類似的,求解三元一次方程組,把它轉化為解二元一次方程組.求解一元二次方程,把它轉化為兩個一元一次方程來解.求解分式方程,把它轉化為整式方程來解,由于“去分母”可能產生增根,所以解分式方程必須檢驗.各類方程的解法不盡相同,但是它們有一個共同的基本數學思想轉化,把未知轉化為已知.用“轉化”的數學思想,我們還可以解一些新的方程.例如,一元三次方程![]() ,可以通過因式分解把它轉化為
,可以通過因式分解把它轉化為![]() ,可得
,可得![]() ,所以x=0或x+2=0或x-1=0,所以方程:
,所以x=0或x+2=0或x-1=0,所以方程:![]() 的解是x1=0,x2=-2,x3=1;
的解是x1=0,x2=-2,x3=1;
(1)問題:用“轉化”思想求方程![]() 的解
的解
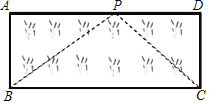
(2)應用:如圖,已知矩形草坪ABCD的長AD=8m,寬AB=3m,小華把一根長為10m的繩子的一端固定在點B,沿草坪邊沿BA,AD走到點P處,把長繩PB段拉直并固定在點P,然后沿草坪邊沿PD、DC走到點C處,把長繩剩下的一段拉直,長繩的另一端恰好落在點C.求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標平面內,![]() 為原點,點
為原點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 軸. 點
軸. 點![]() 與點
與點![]() 關于原點對稱,直線
關于原點對稱,直線![]() (
(![]() 為常數)經過點
為常數)經過點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() .
.
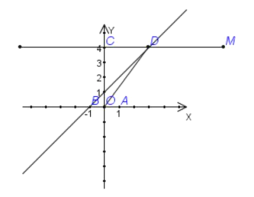
(1)求![]() 的值和點
的值和點![]() 的坐標;
的坐標;
(2)在![]() 軸上有一點
軸上有一點![]() ,使
,使![]() 的面積為
的面積為![]() ,求
,求![]() 點的坐標;
點的坐標;
(3)在![]() 軸的正半軸上是否存在一點
軸的正半軸上是否存在一點![]() ,使得
,使得![]() 為等腰三角形,若存在,求出點
為等腰三角形,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某區為調查學生的視力變化情況,從全區九年級學生中抽取了部分學生,統計了每個人連續三年視力檢查的結果,并將所得數據處理后,制成折線統計圖和扇形統計圖如下:
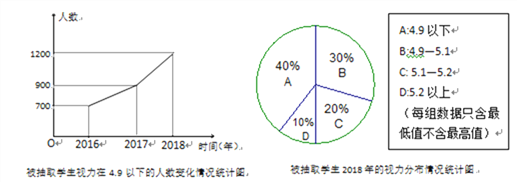
解答下列問題:
(1)該區共抽取了多少名九年級學生?
(2)若該區共有9萬名九年級學生,請你估計2018年該區視力不良(4.9以下)的該年級學生大有多少人?
(3)扇形統計圖中B的圓心角度數為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,現有兩條鄉村公路AB、BC,AB長為1200米,BC長為1600,一個人騎摩托車從A處以20m/s的速度勻速沿公路AB、BC向C處行駛;另一人騎自行車從B處以5m/s的速度從B向C行駛,并且兩人同時出發.
(1)求經過多少秒摩托車追上自行車?
(2)求兩人均在行駛途中時,經過多少秒兩人在行進路線上相距150米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有 A 、B 、C 、D 四個點,分別對應的數為 a ,b , c , d ,且滿足 a ,b 是方程| x7|1的兩個解(a b),且(c 12)2 與| d 16 |互為相反數.

(1)填空: a 、b 、 c 、 d ;
(2)若線段 AB 以 3 個單位/ 秒的速度向右勻速運動,同時線段CD 以 1 單位長度/ 秒向左勻速運動,并設運動時間為t 秒,A 、B 兩點都運動在線段CD 上(不與C , D 兩個端點重合),若BD2AC ,求t 的值;
(3)在(2)的條件下,線段 AB ,線段CD 繼續運動,當點 B 運動到點 D 的右側時,問是否存在時間t ,使 BC3AD ?若存在,求t 的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com