
【題目】我們用[a]表示不大于a的最大整數,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整數,例如:<2.5>=3,<4>=5,<-1.5>=-1.
解決下列問題:
(1)[-4.5]=___,<3.5>=___;
(2)若[x]=2,則x的取值范圍是___;若<y>=-1,則y的取值范圍是___.
(3)已知x,y滿足方程組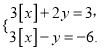 求x,y的取值范圍.
求x,y的取值范圍.
【答案】 (1)-5,4 (2)2≤x<3,-2≤y<-1 (3)-1≤x<0, 2≤y<3.
【解析】【試題分析】(1)根據[a]表示不大于a的最大整數,則[-4.5]=-5,; <a>表示大于a的最小整數,<3.5>=4;
(2)根據[a]表示不大于a的最大整數,因為 [x]=2,所以2≤x<3; <a>表示大于a的最小整數,<y>=-1,則-2≤y<-1;
(3)解方程組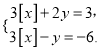 得:得
得:得![]() 再根據其定義,得-1≤x<0,
再根據其定義,得-1≤x<0,
2≤y<3.
【試題解析】
(1)根據定義,得:[-4.5]=-5,<3.5>=4;
(2)根據定義,得:2≤x<3 -2≤y<-1
根據定義得:2≤x<3;-2≤y<-1.
(3)解方程組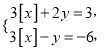 得
得![]()
根據定義得:-1≤x<0; 2≤y<3.


科目:初中數學 來源: 題型:
【題目】對非負實數x“四舍五入”到個位的值記為<x>,即當n為非負整數時,若![]() ,則<x>=n,如<0.46>=0,<3.67>=4。給出下列關于<x>的結論:
,則<x>=n,如<0.46>=0,<3.67>=4。給出下列關于<x>的結論:
①<1.493>=1;
②<2x>=2<x>;
③若![]() ,則實數x的取值范圍是
,則實數x的取值范圍是![]() ;
;
④當x≥0,m為非負整數時,有![]() ;
;
⑤![]() 。
。
其中,正確的結論有 (填寫所有正確的序號)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ABC和∠ACB的角平分線BE、CF相交于點I,

(1)∠BIC=120°,求∠A的度數
(2)當∠BIC=135°,則∠A= 。
(3)請你用數學表達式歸納出∠BIC與∠A的關系式,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形ABCD中,G是AD延長線上的一點,且DG=AD,動點M從A點出發,以每秒1個單位的速度沿著A→C→G的路線向G點勻速運動(M不與A,G重合),設運動時間為t秒,連接BM并延長AG于N.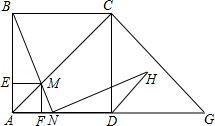
(1)是否存在點M,使△ABM為等腰三角形?若存在,分析點M的位置;若不存在,請說明理由;
(2)當點N在AD邊上時,若BN⊥HN,NH交∠CDG的平分線于H,求證:BN=HN;
(3)過點M分別作AB,AD的垂線,垂足分別為E,F,矩形AEMF與△ACG重疊部分的面積為S,求S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解.并規定:F(n)=![]() .
.
例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=![]() .
.
⑴如果一個正整數m是另外一個正整數n的平方,我們稱正整數m是完全平方數.
求證:對任意一個完全平方數m,總有F(m)=1;
⑵如果一個兩位正整數t,t =10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為54,那么我們稱這個數t為“吉祥數”,求所有的“吉祥數”;
⑶在⑵所得“吉祥數”中,求 F(t)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下四個命題:
①反比例函數y=![]() ,當x>0時,y隨x的增大而增大;
,當x>0時,y隨x的增大而增大;
②拋物線y=x2﹣2x+2與兩坐標軸無交點;
③平分弦的直徑垂直于弦,且平分弦所對的弧;
④有一個角相等的兩個等腰三角形相似.
其中正確命題的個數為( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如下檢測公路上行駛的汽車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道L上確定點D,使CD與L垂直,測得CD的長等于24米,在L上點D的同側取點A、B,使∠CAD=30°,∠CBD=60°. 
(1)求AB的長(結果保留根號);
(2)已知本路段對校車限速為45千米/小時,若測得某輛校車從A到B用時2秒,這輛校車是否超速?說明理由.(參考數據: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,F為CD上一點,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度數為整數,則∠C的度數為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種商品因換季準備打折出售,如果按照原定價的七五折出售,每件將賠25元,而按原定價的九折出售,每件將賺20元,則這種商品的原定價是( )
A.200元B.300元C.320元D.360元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com