
【題目】如圖,在平行四邊形ABCD中,E,F為BC上兩點,且BE=CF,AF=DE.
求證:(1)△ABF≌△DCE;

【答案】(1)∵BE=CF,BF=BE+EF,CE=CF+EF,∴BF=CE.
∵四邊形ABCD是平行四邊形,∴AB=DC.
在△ABF和△DCE中,∵AB=DC,BF=CE,AF=DE,
∴△ABF≌△DCE.
(2)∵△ABF≌△DCE,∴∠B=∠C.
∵四邊形ABCD是平行四邊形,∴AB∥CD.
∴∠B+∠C=180°.
∴∠B=∠C=90°.
∴四邊形ABCD是矩形.
【解析】(1)根據等量代換得到BE=CF,根據平行四邊形的性質得AB=DC.利用“SSS”得△ABF≌△DCE.
(2)平行四邊形的性質得到兩邊平行,從而∠B+∠C=180°.利用全等得∠B=∠C,從而得到一個直角,問題得證.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,E,F分別是BC,AC的中點,以AC為斜邊作Rt△ADC,若∠CAD=∠CAB=45°,則下列結論不正確的是( ) 
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= ![]() CD
CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】①下午 2 點 10 分時,鐘表的時針和分針所成銳角是________;
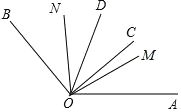
②如圖,射線 OC,OD 在∠AOB 的內部,射線 OM,ON 分別平分∠AOD,∠BOC, 且∠BON=50°,∠AOM=40°,∠COD=30°,則∠AOB 的度數為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)5﹣(﹣3)+(﹣2)﹣1;
(2)2![]() ×(﹣
×(﹣![]() )÷(﹣3);
)÷(﹣3);
(3)﹣5×[1﹣(0.5+ ![]() )÷
)÷![]() ];
];
(4)20×(﹣![]() )+4×(﹣
)+4×(﹣![]() )+2×(﹣
)+2×(﹣![]() );
);
(5)﹣14-(![]() )÷(﹣
)÷(﹣![]() )×[﹣2﹣(﹣3)2]﹣(
)×[﹣2﹣(﹣3)2]﹣(![]() ﹣0.52).
﹣0.52).
查看答案和解析>>
科目:初中數學 來源: 題型:
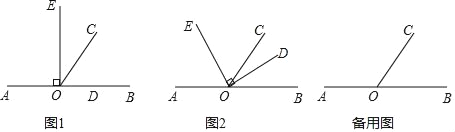
【題目】如圖所示,在直線AB上的一點O,以O為端點依次作射線OE,OC,OD,使∠EOD=90°,∠COB=60°
(1)如圖1當∠EOD的一邊OD在射線OB上時,求∠COE的度數;
(2)如圖2當∠EOD繞著點O逆時針旋轉到OC平分∠BOE時,求∠COD的度數;
(3)當∠EOD繞著點O逆時針旋轉,且O°<∠AOE<90°(但≠60°)時,試猜想∠AOE與∠COD有怎樣的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 的解析表達式為:y=-3x+3,且
的解析表達式為:y=-3x+3,且![]() 與x軸交于點D,直線
與x軸交于點D,直線![]() 經過點A,B,直線
經過點A,B,直線![]() ,
,![]() 交于點C.
交于點C.
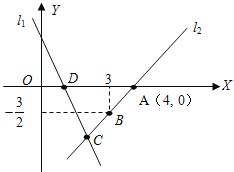
(1)求點D的坐標;
(2)求直線![]() 的解析表達式;
的解析表達式;
(3)求△ADC的面積;
(4)在直線![]() 上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列多面體,并把下表補充完整.
名稱 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
圖形 |
|
|
|
|
頂點數 | 6 | 10 | 12 | |
棱數 | 9 | 12 | ||
面數 | 5 | 8 |
觀察上表中的結果,你能發現![]() 、
、![]() 、
、之間有什么關系嗎?請寫出關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上,點 A 的初始位置表示的數為 1,現點 A 做如下移動:第 1 次點 A 向左移動 3 個單位長度至點 A1,第 2 次從點 A1 向右移動 6 個單位長度至點 A2,第 3 次從點 A2 向左移動 9 個單位長度至點 A3,…,按照這種移動方式進行下去,點 A4 表示的數,是__________ ,如果點 An 與原點的距離不小于 20, 那么 n 的最小值是________________ .
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條不完整的數軸上從左到右有點A,B,C,其中AB=2,BC=1,如圖所示,設點A,B,C所對應數的和是p. ![]()
(1)若以B為原點,寫出點A,C所對應的數,并計算p的值;若以C為原點,p又是多少?
(2)若原點O在圖中數軸上點C的右邊,且CO=28,求p.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com