
【題目】如圖,在平面直角坐標系中,頂點為A(1,﹣1)的拋物線經過點B(5,3),且與x軸交于C,D兩點(點C在點D的左側).
(1)求拋物線的解析式;
(2)求點O到直線AB的距離;
(3)點M在第二象限內的拋物線上,點N在x軸上,且∠MND=∠OAB,當△DMN與△OAB相似時,請你直接寫出點M的坐標.
【答案】
(1)
解:(1)設拋物線的解析式為y=a(x﹣1)2﹣1,
將B點坐標代入函數解析式,得
(5﹣1)2a﹣1=3,
解得a=![]() .
.
故拋物線的解析式為y=![]() (x﹣1)2﹣1
(x﹣1)2﹣1
(2)
由勾股定理,得OA2=11+12=2,OB2=52+32=34,AB2=(5﹣1)2+(3+1)2=32,
OA2+AB2=OB2,
∴∠OAB=90°,
O到直線AB的距離是OA=![]()
(3)
設M(a,b),N(a,0)
當y=0時,![]() (x﹣1)2﹣1=0,
(x﹣1)2﹣1=0,
解得x1=3,x2=﹣1,
D(3,0),DN=3﹣a.
①當△MND∽△OAB時,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
化簡,得4b=a﹣3 ①
M在拋物線上,得b=![]() (a﹣1)2﹣1 ②
(a﹣1)2﹣1 ②
聯立①②,得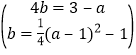 ,
,
解得a1=3(不符合題意,舍),a2=﹣2,b=![]() ,
,
M1(﹣2,![]() ),
),
當△MND∽△BAO時,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
化簡,得b=12﹣4a ③,
聯立②③,得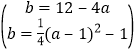 ,
,
解得a1=3(不符合題意,舍),a2=﹣17,b=12﹣4×(﹣17)=80,
M2(﹣17,80).
綜上所述:當△DMN與△OAB相似時,點M的坐標(﹣2,![]() ),(﹣17,80)
),(﹣17,80)
【解析】(1)根據待定系數法,可得拋物線的解析式;
(2)根據勾股定理,可得OA2、OB2、AB2的長,根據勾股定理的逆定理,可得∠OAB等于90°,根據點到直線的距離的定義,可得答案;
(3)根據拋物線上的點滿足函數解析式,可得方程②,根據相似三角形的性質,可得方程①③,根據解方程組,可得M點的坐標


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,且過點A(3,0),二次函數圖象的對稱軸是直線x=1,下列結論正確的是( )
A.![]()
B.ac>0
C.2a﹣b=0
D.a﹣b+c=0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=﹣![]() x2+bx+c,經過A(0,﹣4),B(x1 , 0),C(x2 , 0)三點,且|x2﹣x1|=5.
x2+bx+c,經過A(0,﹣4),B(x1 , 0),C(x2 , 0)三點,且|x2﹣x1|=5.
(1)求b,c的值;
(2)在拋物線上求一點D,使得四邊形BDCE是以BC為對角線的菱形;
(3)在拋物線上是否存在一點P,使得四邊形BPOH是以OB為對角線的菱形?若存在,求出點P的坐標,并判斷這個菱形是否為正方形?若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一組數據1,2,3,…,n(從左往右數,第1個數是1,第2個數是2,第3個數是3,依此類推,第n個數是n).設這組數據的各數之和是s,中位數是k,則s= (用只含有k的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是雙曲線![]() 在第一象限的分支上的一個動點,連接AO并延長交另一分支于點B,過點A作y軸的垂線,過點B作x軸的垂線,兩垂線交于點C,隨著點A的運動,點C的位置也隨之變化.設點C的坐標為(m,n),則m,n滿足的關系式為( )
在第一象限的分支上的一個動點,連接AO并延長交另一分支于點B,過點A作y軸的垂線,過點B作x軸的垂線,兩垂線交于點C,隨著點A的運動,點C的位置也隨之變化.設點C的坐標為(m,n),則m,n滿足的關系式為( )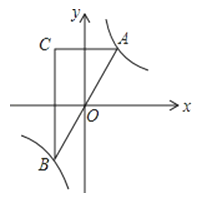
A.n=﹣2m
B.n=![]()
C.n=﹣4m
D.n=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖(1)是一個蒙古包的照片,這個蒙古包可以近似看成是圓錐和圓柱組成的幾何體,如圖(2)所示.
(1)請畫出這個幾何體的俯視圖;
(2)圖(3)是這個幾何體的正面示意圖,已知蒙古包的頂部離地面的高度EO1=6米,圓柱部分的高OO1=4米,底面圓的直徑BC=8米,求∠EAO的度數(結果精確到0.1°).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在我市實施“城鄉環境綜合治理”期間,某校組織學生開展“走出校門,服務社會”的公益活動.八年級一班王浩根據本班同學參加這次活動的情況,制作了如下的統計圖表: 該班學生參加各項服務的頻數、頻率統計表:
服務類別 | 頻數 | 頻率 |
文明宣傳員 | 4 | 0.08 |
文明勸導員 | 10 | |
義務小警衛 | 8 | 0.16 |
環境小衛士 | 0.32 | |
小小活雷鋒 | 12 | 0.24 |
請根據上面的統計圖表,解答下列問題: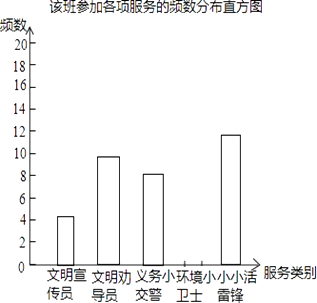
(1)該班參加這次公益活動的學生共有名;
(2)請補全頻數、頻率統計表和頻數分布直方圖;
(3)若八年級共有900名學生報名參加了這次公益活動,試估計參加文明勸導的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com