Question

【題目】如圖，若AB∥CD，在下列三種情況下探究∠APC與∠PAB，∠PCD的數量關系．

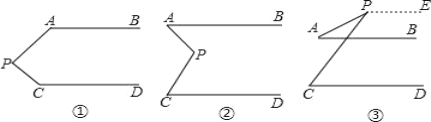
（1）圖①中，∠APC+∠PAB+∠PCD=　 　 ；

（2）圖②中，　　 ；

（3）圖③中，寫出∠APC與∠PAB，∠PCD的三者數量關系，并說明理由

Answer 1

【答案】（1）360°

（2）∠APC=∠PAB+∠PCD

（3）∠APC+∠PAB=∠PCD，理由見解析.

【解析】試題分析：三個圖形中過P作PE與AB平行，由AB與CD平行，利用平行于同一條直線的兩直線平行得到PE與CD平行，利用平行線的性質判斷即可得到結果．

試題解析：（1）過P作PE∥AB，如圖①

∵AB∥CD，

∴PE∥CD，

∴∠A+∠APE=180°，∠EPC+∠C=180°，

∴∠APC+∠PAB+∠PCD=∠A+∠APE+∠EPC+∠C=360°；

（2）過P作PE∥AB，如圖②

∵AB∥CD，

∴PE∥CD，

∴∠A=∠APE，∠EPC=∠C，

∴∠APC=∠APE+∠EPC=∠PAB+∠PCD；

（3）∠APC=∠PCD-∠PAB，

理由為：過P作PE∥AB，如圖③

∵AB∥CD，

∴PE∥CD，

∴∠PAB+∠APE=180°，∠EPC+∠PCD=180°，

即∠APE=180°-∠PAB，∠EPC=180°-∠PCD，

∴∠APC=∠APE-∠EPC=∠PCD-∠PAB．