
【題目】如圖,花叢中有一路燈桿AB,在燈光下,大華在D點處的影長DE=3米,沿BD方向行走到達G點,DG=5米,這時大華的影長GH=5米.如果大華的身高為2米,求路燈桿AB的高度.
【答案】解:∵CD∥AB, ∴△EAB∽△ECD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ①,
①,
∵FG∥AB,
∴△HFG∽△HAB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ②,
②,
由①②得 ![]() =
= ![]() ,
,
解得BD=7.5,
∴ ![]() =
= ![]() ,
,
解得:AB=7.
答:路燈桿AB的高度為7m.
【解析】根據已知易證CD∥AB,FG∥AB,再根據相似三角形的判定定理,即可證出△EAB∽△ECD,△HFG∽△HAB,根據相似三角形的性質,分別得出對應邊成比例,建立方程組,解方程組求出BD、AB的值即可。
【考點精析】本題主要考查了平行線分線段成比例和相似三角形的判定與性質的相關知識點,需要掌握三條平行線截兩條直線,所得的對應線段成比例;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】已知:甲、乙兩車分別從相距300千米的A,B兩地同時出發相向而行,甲到B地后立即返回,下圖是它們離各自出發地的距離y(千米)與行駛時間x(小時)之間的函數圖象.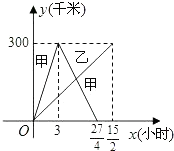
(1)請直接寫出甲、乙兩車離各自出發地的距離y(千米)與行駛時間x(小時)之間的函數關系式,并標明自變量x的取值范圍;
(2)它們在行駛的過程中有幾次相遇?并求出每次相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校九年級學生的理化實驗操作情況,隨機抽查了 ![]() 名同學實驗操作的得分(滿分10分).根據獲取的樣本數據,制作了如下的條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
名同學實驗操作的得分(滿分10分).根據獲取的樣本數據,制作了如下的條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:

(1)扇形①的圓心角的大小是 ;
(2)求這個樣本的容量和樣本數據的平均數;
(3)若該校九年級共有 ![]() 名學生,估計該校理化實驗操作得滿分的學生有多少人.
名學生,估計該校理化實驗操作得滿分的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是四邊形ABCD的對角線BD上一點,且∠BAC=∠BDC=∠DAE.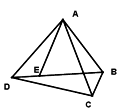
①試說明BE·AD=CD·AE;
②根據圖形特點,猜想 ![]() 可能等于哪兩條線段的比?并證明你的猜想,(只須寫出有線段的一組即可)
可能等于哪兩條線段的比?并證明你的猜想,(只須寫出有線段的一組即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索與應用.先填寫下表,通過觀察后再回答問題:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)從表格中探究a與![]() 數位的規律,并利用這個規律解決下面兩個問題:
數位的規律,并利用這個規律解決下面兩個問題:
①已知![]() ≈3.16,則
≈3.16,則![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,則a= ;
=180,則a= ;
(3)拓展:已知![]() ,若
,若![]() ,則b= .
,則b= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寒梅中學為了豐富學生的課余生活,計劃購買圍棋和中國象棋供棋類興趣小組活動使用,若購買3副圍棋和5副中國象棋需用98元;若購買8副圍棋和3副中國象棋需用158元;(1)求每副圍棋和每副中國象棋各多少元;(2)寒梅中學決定購買圍棋和中國象棋共40副,總費用不超過550元,那么寒梅中學最多可以購買多少副圍棋?
查看答案和解析>>
科目:初中數學 來源: 題型:
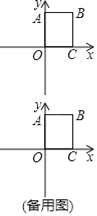
【題目】如圖,在平面直角坐標系中,四邊形OABC為矩形,點A(0,8),C(6,0).動點P從點B出發,以每秒1個單位長的速度沿射線BC方向勻速運動,設運動時間為t秒.
(1)當t= s時,以OB、OP為鄰邊的平行四邊形是菱形;
(2)當點P在OB的垂直平分線上時,求t的值;
(3)將△OBP沿直線OP翻折,使點B的對應點D恰好落在x軸上,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com