
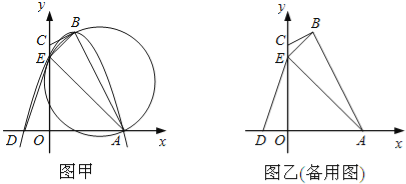
【題目】如圖甲,四邊形OABC的邊OA、OC分別在x軸、y軸的正半軸上,頂點在B點的拋物線交x軸于點A、D,交y軸于點E,連接AB、AE、BE.已知tan∠CBE=![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求拋物線的解析式及頂點B的坐標;
(2)求證:CB是△ABE外接圓的切線;
(3)試探究坐標軸上是否存在一點P,使以D、E、P為頂點的三角形與△ABE相似,若存在,直接寫出點P的坐標;若不存在,請說明理由;
(4)設△AOE沿x軸正方向平移t個單位長度(0<t≤3)時,△AOE與△ABE重疊部分的面積為s,求s與t之間的函數關系式,并指出t的取值范圍.
【答案】(1)y=a(x﹣3)(x+1);點B(1,4)
(2)見解析
(3)見解析
(4)s=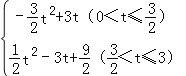
【解析】
(1)由題意,設拋物線解析式為y=a(x﹣3)(x+1).
將E(0,3)代入上式,解得:a=﹣1.
∴y=﹣x2+2x+3.
則點B(1,4).
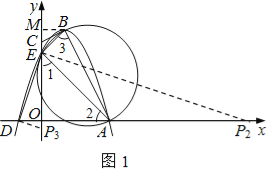
(2)證明:如圖1,過點B作BM⊥y于點M,則M(0,4).
在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE=![]() =3
=3![]() .
.
在Rt△EMB中,EM=OM﹣OE=1=BM,
∴∠MEB=∠MBE=45°,BE=![]() =
=![]() .
.
∴∠BEA=180°﹣∠1﹣∠MEB=90°.
∴AB是△ABE外接圓的直徑.
在Rt△ABE中,tan∠BAE=![]() =
=![]() =tan∠CBE,
=tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圓的切線.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=![]() ,sin∠BAE=
,sin∠BAE=![]() ,cos∠BAE=
,cos∠BAE=![]() ;
;
若以D、E、P為頂點的三角形與△ABE相似,則△DEP必為直角三角形;
①DE為斜邊時,P1在x軸上,此時P1與O重合;
由D(﹣1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO=![]() =tan∠BAE,即∠DEO=∠BAE
=tan∠BAE,即∠DEO=∠BAE
滿足△DEO∽△BAE的條件,因此 O點是符合條件的P1點,坐標為(0,0).
②DE為短直角邊時,P2在x軸上;
若以D、E、P為頂點的三角形與△ABE相似,則∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=![]() ;
;
而DE=![]() =
=![]() ,則DP2=DE÷sin∠DP2E=
,則DP2=DE÷sin∠DP2E=![]() ÷
÷![]() =10,OP2=DP2﹣OD=9
=10,OP2=DP2﹣OD=9
即:P2(9,0);
③DE為長直角邊時,點P3在y軸上;
若以D、E、P為頂點的三角形與△ABE相似,則∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=![]() ;
;
則EP3=DE÷cos∠DEP3=![]() ÷
÷![]() =
=![]() ,OP3=EP3﹣OE=
,OP3=EP3﹣OE=![]() ;
;
綜上,得:P1(0,0),P2(9,0),P3(0,﹣![]() ).
).
(4)解:設直線AB的解析式為y=kx+b.
將A(3,0),B(1,4)代入,得![]() 解得
解得![]()
∴y=﹣2x+6.
過點E作射線EF∥x軸交AB于點F,當y=3時,得x=![]() ,∴F(
,∴F(![]() ,3).
,3).
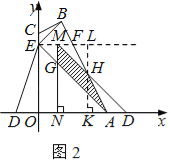
情況一:如圖2,當0<t≤![]() 時,設△AOE平移到△DNM的位置,MD交AB于點H,MN交AE于點G.
時,設△AOE平移到△DNM的位置,MD交AB于點H,MN交AE于點G.
則ON=AD=t,過點H作LK⊥x軸于點K,交EF于點L.
由△AHD∽△FHM,得![]() ,即
,即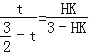 .
.
解得HK=2t.
∴S陰=S△MND﹣S△GNA﹣S△HAD=![]() ×3×3﹣
×3×3﹣![]() (3﹣t)2﹣
(3﹣t)2﹣![]() t2t=﹣
t2t=﹣![]() t2+3t.
t2+3t.
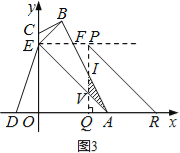
情況二:如圖3,當![]() <t≤3時,設△AOE平移到△PQR的位置,PQ交AB于點I,交AE于點V.
<t≤3時,設△AOE平移到△PQR的位置,PQ交AB于點I,交AE于點V.
由△IQA∽△IPF,得![]() .即
.即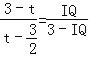 ,
,
解得IQ=2(3﹣t).
∴S陰=S△IQA﹣S△VQA=![]() ×(3﹣t)×2(3﹣t)﹣
×(3﹣t)×2(3﹣t)﹣![]() (3﹣t)2=
(3﹣t)2=![]() (3﹣t)2=
(3﹣t)2=![]() t2﹣3t+
t2﹣3t+![]() .
.
綜上所述:s=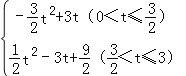 .
.


 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
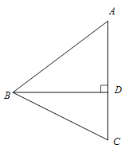
【題目】如圖,在△ABC中,AB=AC>BC,BD 是AC邊上的高,點C關于直線BD的對稱點為點E,連接BE.
(1)①依題意補全圖形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,點F是BE中點,連接AF,BD=4,求AF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=m,P為BC上任意一點,則PA2+PBPC的值為( )
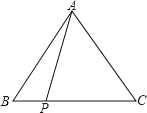
A. m2 B. m2+1 C. 2m2 D. (m+1)2
查看答案和解析>>
科目:初中數學 來源: 題型:
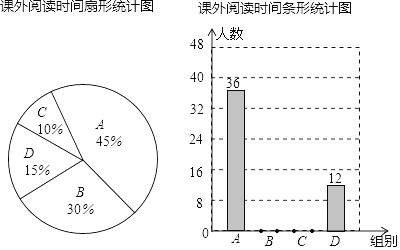
【題目】為了創建書香校園,切實引導學生多讀書,讀好書.某中學開展了“好書伴我成長”的讀書節活動,為了了解本校學生每周課外閱讀時間,隨機抽取部分學生進行問卷調查,將課外閱讀時間分為A、B、C、D四組,并利用臭氧所得的數據繪制了如下統計圖.
組別 | 課外閱讀t(單位:時) |
A | X<2 |
B | 2≤x<3 |
C | 3≤x<4 |
D | x≥4 |
請根據圖中提供的信息,解答下列問題:
(1)一共調查了________名學生;
(2)扇形統計圖中A組的圓心角度數________;
(3)直接補全條形統計圖
(4)若該校有2400名學生,根據你所調查的結果,估計每周課外閱讀時間不足3小時的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
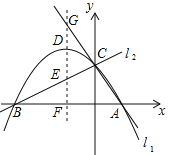
【題目】(2017四川省巴中市,第31題,12分)如圖,已知兩直線l1,l2分別經過點A(1,0),點B(﹣3,0),且兩條直線相交于y軸的正半軸上的點C,當點C的坐標為(0,![]() )時,恰好有l1⊥l2,經過點A、B、C的拋物線的對稱軸與l1、l2、x軸分別交于點G、E、F,D為拋物線的頂點.
)時,恰好有l1⊥l2,經過點A、B、C的拋物線的對稱軸與l1、l2、x軸分別交于點G、E、F,D為拋物線的頂點.
(1)求拋物線的函數解析式;
(2)試說明DG與DE的數量關系?并說明理由;
(3)若直線l2繞點C旋轉時,與拋物線的另一個交點為M,當△MCG為等腰三角形時,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各圖中的MA1與NAn平行.
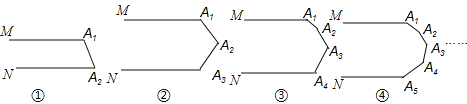
(1)圖①中的∠A1+∠A2= 度,圖②中的∠A1+∠A2+∠A3= 度,
圖③中的∠A1+∠A2+∠A3+∠A4= 度,圖④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩個圖中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n個圖中的∠A1+∠A2+∠A3+…+∠An= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家新開發的一種電動車如圖,它的大燈A射出的光線AB,AC與地面MN所夾的銳角分別為8°和10°,大燈A與地面離地面的距離為1m求該車大燈照亮地面的寬度BC.(不考慮其它因素)(參數數據:sin8°=![]() ,tan8°=
,tan8°=![]() ,sin10°=
,sin10°=![]() ,tan10°=
,tan10°=![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
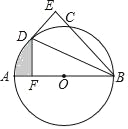
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,∠ABC的平分線交⊙O于點D,DE⊥BC于點E.
(1)試判斷DE與⊙O的位置關系,并說明理由;
(2)過點D作DF⊥AB于點F,若BE=3![]() ,DF=3,求圖中陰影部分的面積.
,DF=3,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點![]() 在反比例函數
在反比例函數![]() 的圖象上,過點
的圖象上,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,直線
,直線![]() 經過點
經過點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函數![]() 和一次函數
和一次函數![]() 的表達式;
的表達式;
(2)直接寫出關于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com