
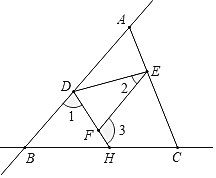
【題目】如圖,直線AB和直線BC相交于點B,連接AC,點D、E、H分別在AB、AC、BC上,連接DE、DH,F是DH上一點,已知∠1+∠3=180°.
(1)求證:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=![]() 求∠3的度數(用含
求∠3的度數(用含![]() 的代數式表示).
的代數式表示).
 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】今年南方某地發生特大洪災,政府為了盡快搭建板房安置災民,給某廠下達了生產A種板材48000㎡和B種板材24000㎡的任務.
⑴如果該廠安排210人生產這兩種材,每人每天能生產A種板材60㎡或B種板材40㎡,請問:應分
別安排多少人生產A種板材和B種板材,才能確保同時完成各自的生產任務?
⑵某災民安置點計劃用該廠生產的兩種板材搭建甲、乙兩種規格的板房共400間,已知建設一間甲型板房和一間乙型板房所需板材及安置人數如下表所示:
板房 | A種板材(m2) | B種板材(m2) | 安置人數 |
甲型 | 108 | 61 | 12 |
乙型 | 156 | 51 | 10 |
問這400間板房最多能安置多少災民?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,∠A=40°.點P是射線AB上一動點(與點A不重合),CE、CF分別平分∠ACP和∠DCP交射線AB于點E、F.
(1)求∠ECF的度數;
(2)隨著點P的運動,∠APC與∠AFC之間的數量關系是否改變?若不改變,請求出此數量關系;若改變,請說明理由;
(3)當∠AEC=∠ACF時,求∠APC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在初三綜合素質評定結束后,為了了解年級的評定情況,現對初三某班的學生進行了評定等級的調查,繪制了如下男女生等級情況折線統計圖和全班等級情況扇形統計圖.
(1)調查發現評定等級為合格的男生有2人,女生有1人,則全班共有名學生.
(2)補全女生等級評定的折線統計圖.
(3)根據調查情況,該班班主任從評定等級為合格和A的學生中各選1名學生進行交流,請用樹形圖或表格求出剛好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】假期,某校為了勤工儉學,要完成整個A小區的綠化工作,開始由七年級單獨工作了4天,完成整個綠化工作的三分之一,這時九年級也參加工作,兩個年級又共同工作了2天,才全部完成整個綠化工作,則由九年級單獨完成整個綠化工作需要____天.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數據x1,x2,…,xn的方差為A,則數據3x1+1,3x2+1,…3xn+1的方差為( )
A. 3A B. 3A+1 C. 9A D. 9A+1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在A市正北300km處有B市,(1)以A市為原點,東西方向的直線為x軸,南北方向的直線為y軸,并以100km為1個單位建立平面直角坐標系.
(2)根據氣象臺預報,今年7號臺風中心位置現在C(5,2)處,并以60千米/時的速度自東向西移動,臺風影響范圍半徑為200km,問經幾小時后,B市將受到臺風影響?并畫出示意圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地震救援隊探測出某建筑物廢墟下方點C處有生命跡象,已知廢墟一側地面上兩探測點A,B相距3米,探測線與地面的夾角分別是30°和60°(如圖),試確定生命所在點C的深度.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索與應用.先填寫下表,通過觀察后再回答問題:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)從表格中探究a與![]() 數位的規律,并利用這個規律解決下面兩個問題:
數位的規律,并利用這個規律解決下面兩個問題:
①已知![]() ≈3.16,則
≈3.16,則![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,則a= ;
=180,則a= ;
(3)拓展:已知![]() ,若
,若![]() ,則b= .
,則b= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com