
【題目】如圖,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)請問BD和CE是否平行?請你說明理由;
(2)AC和BD有何位置關系?請你說明判斷的理由。
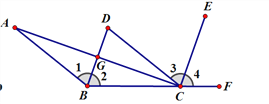
【答案】(1) BD∥CE;(2) AC和BD垂直
【解析】試題分析:(1)根據平行線性質得出∠ABC=∠DCF,根據角平分線定義求出∠2=∠4,根據平行線的判定推出即可;
(2)根據平行線性質得出∠DGC+∠ACE=180°,根據∠ACE=90°,求出∠DGC=90°,根據垂直定義推出即可.
試題解析:(1)BD∥CE.
理由:∵AB∥CD,
∴∠ABC=∠DCF,
∴BD平分∠ABC,CE平分∠DCF,
∴∠2=![]() ∠ABC,∠4=
∠ABC,∠4=![]() ∠DCF,
∠DCF,
∴∠2=∠4,
∴BD∥CE(同位角相等,兩直線平行);
(2)AC⊥BD,
理由:∵BD∥CE,
∴∠DGC+∠ACE=180°,
∴∠ACE=90°,
∴∠DGC=180°-90°=90°,
即AC⊥BD.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】金庸先生筆下的“五岳劍派”就是在以下五大名山中:
山名 | “東岳泰山” | “西岳華山” | “南岳衡山” | “北岳恒山” | “中岳嵩山” |
海拔(米) | 1545 | 2155 | 1300 | 2016 | 1491 |
若想根據表中數據繪制統計圖,以便更清楚的比較這五座山的高度,最合適的是( )
A.扇形統計圖B.折線統計圖C.條形統計圖D.以上都可以
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題14分)如圖,拋物線y=![]() x2+
x2+![]() x+c與x軸的負半軸交于點A,與y軸交于點B,連結AB,點C(6,
x+c與x軸的負半軸交于點A,與y軸交于點B,連結AB,點C(6, ![]() )在拋物線上,直線AC與y軸交于點D.
)在拋物線上,直線AC與y軸交于點D.

(1)求c的值及直線AC的函數表達式;
(2)點P在x軸正半軸上,點Q在y軸正半軸上,連結PQ與直線AC交于點M,連結MO并延長交AB于點N,若M為PQ的中點.
①求證:△APM∽△AON;
②設點M的橫坐標為m,求AN的長(用含m的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖的網格線是由邊長為1的小正方形格子組成的, 小正方形的頂點叫格點,以格點為頂點的多邊形叫格點多邊形,小明研究發現,內部含有3個格點的四邊形的面積與該四邊形邊上的格點數有某種關系,請你觀察圖中的4個格點四邊形.設內部含有3個格點的四邊形的面積為S,其各邊上格點的個數之和為 m,則S與m的關系為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電信公司手機有兩類收費標準,A類收費標準如下:不管通話時間多長,少,每部手機每月必須繳月租費12元,另外,通話費按0.2元/min計。B類收費標準如下:沒有月租費,但通話費按0.25元/min計。
(1)分別寫出A、B兩類每月應繳費用y(元)與通話時間x(min)之間的關系式;
(2)如果手機用戶預算每月交55元的話費,那么該用戶選擇哪類收費方式合算?
(3)每月通話多長時間,按A、B兩類收費標準繳費,所繳話費相等?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的袋子中裝有10個紅球、7個黃球、2個白球,這些球除了顏色外無其他差別.從袋子中隨機摸出一個球,然后放回去繼續摸,如果前三次摸出的都是紅球,那么第四次摸出( )球的可能性最大.
A.紅B.黃C.白D.每種球的可能性一樣大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com