Question

【題目】（本題共12分）如圖，在平面直角坐標系中，頂點為的拋物線交軸于點，交軸于，兩點（點在點的左側）．已知點坐標為．

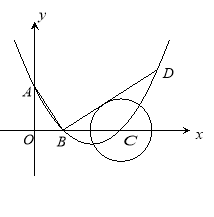
（1）求此拋物線的解析式；

（2） 過點作線段的垂線交拋物線于點， 如果以點為圓心的圓與直線相切，請判斷拋物線的對稱軸與有怎樣的位置關系，并給出證明；

（3）已知點是拋物線上的一個動點，且位于，兩點之間，問：當點運動到什么位置時，的面積最大？并求出此時點的坐標和的最大面積．

Answer 1

【答案】（1）；（2）相交；過程見解析；（3）△PAC的面積最大值為；點的坐標為．

【解析】

試題分析：

（1）首先將拋物線的解析式設成頂點式，然后將點的坐標代入求出函數解析式；

（2）首先根據函數解析式求出點和點的坐標，從而得出的長度，然后設圓與相切于點，連接，根據題意得出和相似，從而得出的長度，然后得出答案；

（3）過點作軸的平行線交于點，求出的解析式，根據函數解析式分別設出點和點的坐標，求出的長度，然后將的面積用含的代數式表示出來，從而根據函數的性質得出最大值．

試題解析：

解:（1）設拋物線為．

∵拋物線經過點，

∴．

∴．

∴拋物線為........（2分）

（2）與相交．

當時，，．

∴為，為........（2分）

∴．

設與相切于點，連接，則．

∵，

∴．

又∵，

∴．

∴

∴．

∴．

∴........（3分）

∵拋物線的對稱軸為，

∴點到的距離為．

∴拋物線的對稱軸與相交........（5分）

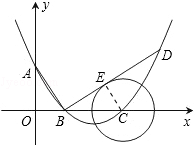
（3）過點作平行于軸的直線交于點．

根據題意可得：的解析式為........（1分）

設點的坐標為（，），則點的坐標為（，）．

∴．

∵........（3分）

∴當時，的面積最大為........（4分）

此時，點的坐標為........（5分）