
【題目】如圖,將平行四邊形ABCD折疊,使頂點D恰落在AB邊上的點M處,折痕為AN,那么下列說法不正確的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
【答案】C
【解析】
根據平行四邊形ABCD,可得∠B=∠D,再根據折疊可得∠D=∠NMA,再利用等量代換可得∠B=∠NMA,然后根據平行線的判定方法可得MN∥BC;首先證明四邊形AMND是平行四邊形,則BM=CN,AD=BC,再根據折疊可得AM=DA,則四邊形AMND為菱形,再根據菱形的性質可得MN=AM.由以上可做出選擇.
解:∵四邊形ABCD是平行四邊形,
∴∠B=∠D,
∵根據折疊可得∠D=∠NMA,
∴∠B=∠NMA,
∴MN∥BC;故A正確;
∵四邊形ABCD是平行四邊形,
∴DN∥AM,AD∥BC,
∵MN∥BC,
∴AD∥MN,
∴四邊形AMND是平行四邊形,
∴BM=CN,AD=BC,
根據折疊可得AM=DA,
∴四邊形AMND為菱形,
∴MN=AM;故B、D正確;
故選:C.


科目:初中數學 來源: 題型:
【題目】閱讀材料,解決下列問題:
材料一:對非負實數x“四舍五入”到個位的值記為![]() ,即:當n為非負整數時,如果
,即:當n為非負整數時,如果![]() ,則
,則![]() ;反之,當n為非負整數時,如果
;反之,當n為非負整數時,如果![]() ;則
;則![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐標系中任意兩點![]() ,
,![]() ,我們把
,我們把![]() 叫做
叫做![]() 、
、![]() 兩點間的折線距離,并規定
兩點間的折線距離,并規定![]() 若
若![]() 是一定點,
是一定點,![]() 是直線
是直線![]() 上的一動點,我們把
上的一動點,我們把![]() 的最小值叫做
的最小值叫做![]() 到直線
到直線![]() 的折線距離,例如:若
的折線距離,例如:若![]() ,
,![]() 則
則![]() .
.
![]() 如果
如果![]() ,寫出實數x的取值范圍;
,寫出實數x的取值范圍;![]() 已知點
已知點![]() ,點
,點![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m為滿足
若m為滿足![]() 的最大值,求點
的最大值,求點![]() 到直線
到直線![]() 的折線距離.
的折線距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠A=∠BCD=90°,BC=DC,延長AD到E,使DE=AB.
(1)求證:∠ABC=∠EDC;
(2)求證:△ABC≌△EDC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數的圖象與反比例函數的圖象交于第二、四象限內的A,B兩點,與x軸交于點C,與y軸交于點D,點B的坐標是(m,﹣4),連接AO,AO=5,sin∠AOC= ![]() .
.
(1)求反比例函數的解析式;
(2)連接OB,求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC.設MN交∠ACB的平分線于點E,交∠ACB的外角平分線于點F.

(1)求證:OE=OF;
(2)若CE=12,CF=5,求OC的長;
(3)當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在Rt△ABC中,∠ACB=90°,D、E分別是AB、AC的中點,F是BC延長線上的一點,且EF∥DC.(1)求證:四邊形CDEF是平行四邊形;(2)若EF=2cm,求AB的長.
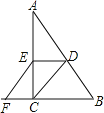
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填空,完成下列說理過程
如圖,點A,O,B在同一條直線上, OD,OE分別平分∠AOC和∠BOC.

(1)求∠DOE的度數;
(2)如果∠COD=65°,求∠AOE的度數.
解:(1)如圖,因為OD是∠AOC的平分線,
所以∠COD =![]() ∠AOC.
∠AOC.
因為OE是∠BOC 的平分線,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于點P(a,b),點Q(c,d),如果a﹣b=c﹣d,那么點P與點Q就叫作等差點.例如:點P(4,2),點Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,則點P與點Q就是等差點.如圖在矩形GHMN中,點H(2,3),點N(﹣2,﹣3),MN⊥y軸,HM⊥x軸,點P是直線y=x+b上的任意一點(點P不在矩形的邊上),若矩形GHMN的邊上存在兩個點與點P是等差點,則b的取值范圍為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線m與直線n垂直相交于O,點A在直線m上運動,點B 在直線n上運動,AC、BC分別是∠BAO和∠ABO的角平分線.
(1)求∠ACB的大小;
(2)如圖2,若BD是△AOB的外角∠OBE的角平分線,BD與AC相交于點D,點A、B在運動的過程中,∠ADB的大小是否會發生變化?若發生變化,請說明理由;若不發生變化,試求出其值;
(3)如圖3,過C作直線與AB交于F,且滿足∠AGO-∠BCF=45°,求證:CF∥OB.
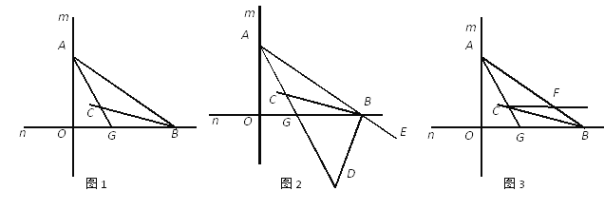
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com