
【題目】如圖,四邊形ABCD為⊙O的內接四邊形,且對角線AC為直徑,AD=BC,過點D作DG⊥AC,垂足為E,DG分別與AB及CB延長線交于點F、M.
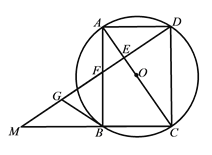
(1)求證:四邊形ABCD是矩形;
(2)若點G為MF的中點,求證:BG是⊙O的切線;
(3)若AD=4,CM=9,求四邊形ABCD的面積.
【答案】(1)證明見解析;(2)證明見解析; (3)S矩形ABCD=24.
【解析】試題分析:(1)根據AC為 O直徑,得到∠ADC=∠CBA=90°,通過全等三角形得到CD=AB,推出四邊形ABCD是平行四邊形,根據矩形的判定定理得到結論;
(2)根據直角三角形的性質得到NB=![]() MF=NF,根據等腰三角形的性質和余角的性質即可得到NB是 O的切線;
MF=NF,根據等腰三角形的性質和余角的性質即可得到NB是 O的切線;
(3)根據四邊形ABCD是矩形,推出△ACD∽△DMC,根據相似三角形的性質列比例式得到![]() ,從而求得DC=6,根據矩形的面積公式即可得到結論.
,從而求得DC=6,根據矩形的面積公式即可得到結論.
試題解析:
(1)證明:∵AC是⊙O的直徑,
∴∠ADC=∠ABC=90°.
在Rt△ADC和Rt△CBA中,
AC=CA,AD=CB,

∴Rt△ADC≌Rt△CBA,
∴∠CAD=∠ACB,
∴AD∥BC,又AD=BC,
∴四邊形ABCD是平行四邊形,又∠ABC=90°,
∴□ABCD是矩形.
(2)證明:連接OB,
在Rt△MBF中,G是MF的中點,
∴BG=![]() MF=FG,
MF=FG,
∴∠GBF=∠GFB=∠AFE.
∵OA=OB,
∴∠OBA=∠OAB.
∵DG⊥AC,
∴∠AFE+∠OAB=90°,
∴∠GBF+∠OBA=90°,
即OB⊥BG,
∴BG是⊙O的切線.
(3)解:由(1)得四邊形ABCD是矩形,
∴∠ADC=∠DCM=90°又AC⊥DG,
∴∠CDM+∠ACD=90°,∠CDM+∠M=90°
∴∠ACD=∠M
又∠ADC=∠DCM,
∴△ACD∽△DMC,
∴![]() ,
,
∴DC2=AD·CM=36,
∴DC=6,
∴S矩形ABCD=AD·CD=24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】對于二次函數y=x2+2x﹣1的圖象與性質,下列說法中正確的是( )
A.頂點坐標為(1,2)
B.當x<﹣1時,y隨x的增大而增大
C.對稱軸是直線x=﹣1
D.最小值是﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,在數軸上點![]() ,
, ![]() 所對應的數是
所對應的數是![]() ,
, ![]() .
.
對于關于![]() 的代數式
的代數式![]() ,我們規定:當有理數
,我們規定:當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,代數式
)的任意一點時,代數式![]() 取得所有值的最大值小于等于
取得所有值的最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,則稱代數式
,則稱代數式![]() ,是線段
,是線段![]() 的封閉代數式.
的封閉代數式.
例如,對于關于![]() 的代數式
的代數式![]() ,當
,當![]() 時,代數式
時,代數式![]() 取得最大值是
取得最大值是![]() ;當
;當![]() 時,代數式
時,代數式![]() 取得最小值是
取得最小值是![]() ,所以代數式
,所以代數式![]() 是線段
是線段![]() 的封閉代數式.
的封閉代數式.
問題:(![]() )關于
)關于![]() 代數式
代數式![]() ,當有理數
,當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,取得的最大值和最小值分別是__________.
)的任意一點時,取得的最大值和最小值分別是__________.
所以代數式![]() __________(填是或不是)線段
__________(填是或不是)線段![]() 的封閉代數式.
的封閉代數式.
(![]() )以下關
)以下關![]() 的代數式:
的代數式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
是線段![]() 的封閉代數式是__________,并證明(只需要證明是線段
的封閉代數式是__________,并證明(只需要證明是線段![]() 的封閉代數式的式子,不是的不需證明).
的封閉代數式的式子,不是的不需證明).
(![]() )關于
)關于![]() 的代數式
的代數式![]() 是線段
是線段![]() 的封閉代數式,則有理數
的封閉代數式,則有理數![]() 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
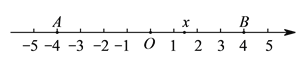
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=kx+2與x軸、y軸分別交于點A(-1,0)和點B,與反比例函數y=![]() 的圖象在第一象限內交于點C(1,n).
的圖象在第一象限內交于點C(1,n).
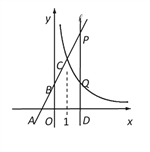
(1)求k的值;
(2)求反比例函數的解析式;
(3)過x軸上的點D(a,0)作平行于y軸的直線![]() (a>1),分別與直線AB和雙曲線
(a>1),分別與直線AB和雙曲線![]() 交于點P、Q,且PQ=2QD,求點D的坐標.
交于點P、Q,且PQ=2QD,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,DG平分∠ADB交AB于點G,GF⊥BD于F.
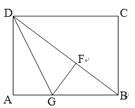
(1)求證:△ADG≌△FDG;(2)若BG=2AG,BD=2![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=mx+4的圖象與x軸相交于點A,與反比例函數y=![]()
![]() 的圖象相交于點B(1,6).
的圖象相交于點B(1,6).
(1)求一次函數和反比例函數的解析式;
(2)設點P是x軸上一點,若S△APB=18,直接寫出點P的坐標.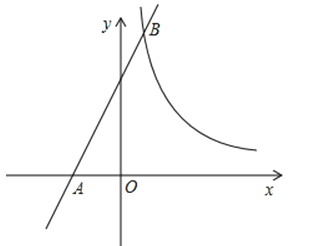
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在同一內有三點![]() 、
、![]() 、
、![]() ,請你根據下列要求用直尺和圓規作圖:
,請你根據下列要求用直尺和圓規作圖:
①畫線段![]() ,
, ![]() .
.
②作射線![]() ,并在射線
,并在射線![]() 上取一點
上取一點![]() ,使
,使![]() .
.
③作射線![]() ,并在射線
,并在射線![]() 上取一點
上取一點![]() ,使
,使![]() .
.
請根據以上作圖,解答下列問題:
(![]() )請問
)請問![]() 、
、![]() 分別是哪兩條線段的中點?并說理由.
分別是哪兩條線段的中點?并說理由.
(![]() )若巳知線段
)若巳知線段![]() 的長為
的長為![]() ,求線段
,求線段![]() 的長度.
的長度.
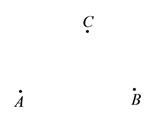
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com