Question

【題目】在平面直角坐標系中，O為坐標原點，A(m,n+1),B(m+2,n).

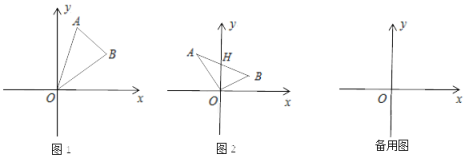
（1）當m=1,n=2時.如圖1，連接AB、AO、BO.直接寫出△ABO的面積為 .

（2）如圖2，若點A在第二象限、點B在第一象限，連接AB、AO、BO,AB交y軸于H，△ABO的面積為2.求點H的坐標.

（3）若點A、B在第一象限，在y 軸正半軸上存在點C，使得∠CAB=900,且CA=AB,求m的值，及OC的長（用含n的式子表示）.

Answer 1

【答案】（1）；（2）點H的坐標（0，2）；（3）OC=n-1（n＞1），m=1

【解析】

（1）過點A作AC⊥y軸于點C，過點B作BD⊥x軸于點D，AC、BD交于點E，求出各點坐標，然后利用△ABO所在矩形的面積減去周圍三角形的面積計算即可；

（2）根據計算即可；

（3）過點A作ADy軸，垂足為D，延長DA，過點B作BEDA，交DA的延長線于點E，首先證明，得到AD=BE=m，CD=AE=2，然后列式計算即可.

（1）如圖，過點A作AC⊥y軸于點C，過點B作BD⊥x軸于點D，AC、BD交于點E，

∵m=1，n=2，

∴A(1，3),B(3，2)，

∴C（0，3），E（3，3），D（3，0），

∴S△ABO；

（2）==OH=2，

點H的坐標（0，2）；

（3）過點A作ADy軸，垂足為D，延長DA，過點B作BEDA，交DA的延長線于點E，

，

，

∠CAB=90°，

，

，

CA=AB，

，

AD=BE=m，CD=AE=2，

OC+CD=n+1，

OC=n-1（n＞1），

OC+CD=n+m=n+1，

m=1.