
【題目】已知如圖,直線AB、CD相交于點O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度數;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度數;
(3)在(2)的條件下,過點O作OF⊥AB,請直接寫出∠EOF的度數. 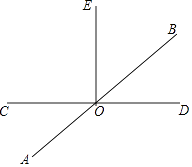
【答案】
(1)解:∵∠AOC=36°,∠COE=90°,
∴∠BOE=180°﹣∠AOC﹣∠COE=54°
(2)解:∵∠BOD:∠BOC=1:5,
∴∠BOD=180°× ![]() =30°,
=30°,
∴∠AOC=30°,
∴∠AOE=30°+90°=120°
(3)解:如圖1,∠EOF=120°﹣90°=30°,
或如圖2,∠EOF=360°﹣120°﹣90°=150°.
故∠EOF的度數是30°或150°.

【解析】(1)根據平角的定義求解即可;(2)根據平角的定義可求∠BOD,根據對頂角的定義可求∠AOC,根據角的和差關系可求∠AOE的度數;(3)先過點O作OF⊥AB,再分兩種情況根據角的和差關系可求∠EOF的度數.


科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,點D是BC上一點,∠BAD=80°,AB=AD=DC,則∠C的大小為( ) 
A.50°
B.40°
C.20°
D.25°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校學生會組織學生到距學校6千米的敬老院打掃衛生,如圖所示,11、12分別表示步行和騎車同學前往目的地所走的路程y(千米)與所用時間x(分鐘)之間的函數圖象,求在距學校多遠處騎車的同學追上步行的同學,此時步行的同學走了多少分鐘? 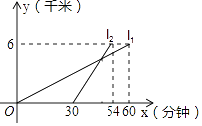
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于x,y定義一種新運算“*”:x*y=3x﹣2y,等式右邊是通常的減法和乘法運算,如2*5=3×2﹣2×5=﹣4,那么(x+1)*(x﹣1)≥5的解集是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線a、b被直線c所截,下列說法正確的是( ) 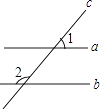
A.當∠1=∠2時,一定有a∥b
B.當a∥b時,一定有∠1=∠2
C.當a∥b時,一定有∠1+∠2=90°
D.當∠1+∠2=180°時,一定有a∥b
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com