
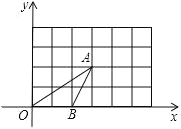
【題目】如圖,△OAB的頂點坐標(biāo)分別為O(0,0)、A(3,2)、B(2,0),將這三個頂點的坐標(biāo)同時擴(kuò)大到原來的2倍,得到對應(yīng)點D、E、F.
(1)在圖中畫出△DEF;
(2)點E是否在直線OA上?為什么?
(3)△OAB與△DEF______位似圖形(填“是”或“不是”)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在長方形 ABCD 中,放入六個形狀大小相同的長方形,所標(biāo)尺寸如圖所示, 則圖中陰影部分面積為( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,三角形ABC的頂點坐標(biāo)分別為![]() ,
,![]() ,
,![]() ,把三角形ABC進(jìn)行平移,平移后得到三角形
,把三角形ABC進(jìn)行平移,平移后得到三角形![]() ,且三角形ABC內(nèi)任意點
,且三角形ABC內(nèi)任意點![]() 平移后的對應(yīng)點為
平移后的對應(yīng)點為![]() .
.
(1)面出平移后的圖形;
(2)三角形ABC是經(jīng)過怎樣平移后得到三角形![]() 的?寫出三個頂點
的?寫出三個頂點![]() ,
,![]() ,
,![]() 的坐標(biāo);
的坐標(biāo);
(3)求三角形ABC的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,等腰Rt△CEF的斜邊CE在正方形ABCD的邊BC的延長線上,CF>BC,取線段AE的中點M 。
(1)求證:MD=MF,MD⊥MF
(2)若Rt△CEF繞點C順時針旋轉(zhuǎn)任意角度(如圖2),其他條件不變。(1)中的結(jié)論是否仍然成立,若成立,請證明,若不成立,請說明理由。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)課上,老師提出一個問題:如圖①,在平面直角坐標(biāo)系中,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 是
是![]() 軸正半軸上一動點,以
軸正半軸上一動點,以![]() 為邊作等腰直角三角形
為邊作等腰直角三角形![]() ,使
,使![]() ,點
,點![]() 在第一象限,設(shè)點
在第一象限,設(shè)點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,設(shè)……為
,設(shè)……為![]() ,
,![]() 與
與![]() 之間的函數(shù)圖象如圖②所示.題中用“……”表示的缺失的條件應(yīng)補為( )
之間的函數(shù)圖象如圖②所示.題中用“……”表示的缺失的條件應(yīng)補為( )


A.點![]() 的橫坐標(biāo)B.點
的橫坐標(biāo)B.點![]() 的縱坐標(biāo)C.
的縱坐標(biāo)C.![]() 的周長D.
的周長D.![]() 的面積
的面積
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】直線![]() 的解析式為
的解析式為![]() ,分別交
,分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() .
.

(1)寫出![]() 兩點的坐標(biāo),并畫出直線
兩點的坐標(biāo),并畫出直線![]() 的圖象.(不需列表);
的圖象.(不需列表);
(2)將直線![]() 向左平移4個單位得到
向左平移4個單位得到![]() 交
交![]() 軸于點
軸于點![]() .作出
.作出![]() 的圖象,
的圖象,![]() 的解析式是___________.
的解析式是___________.
(3)過![]() 的頂點能否畫出直線把
的頂點能否畫出直線把![]() 分成面積相等的兩部分?若能,可以畫出幾條?直接寫出滿足條件的直線解析式.(不必在圖中畫出直線)
分成面積相等的兩部分?若能,可以畫出幾條?直接寫出滿足條件的直線解析式.(不必在圖中畫出直線)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是某小區(qū)的一個健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端點A到地面CD的距離(精確到0.1m).(參考數(shù)據(jù):sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)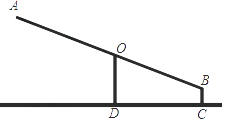
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某家電集團(tuán)公司研制生產(chǎn)的新家電,前期投資 ![]() 萬元,每生產(chǎn)一臺這種新家電,后期還需其他投資
萬元,每生產(chǎn)一臺這種新家電,后期還需其他投資![]() 萬元,已知每臺新家電售價為
萬元,已知每臺新家電售價為 ![]() 萬元,設(shè)總投資為
萬元,設(shè)總投資為![]() 萬元(總投資
萬元(總投資![]() 前期投資
前期投資![]() 后期投資),總利潤為
后期投資),總利潤為![]() 萬元(總利潤
萬元(總利潤![]() 總售價
總售價![]() 總投資),新家電總產(chǎn)量為
總投資),新家電總產(chǎn)量為![]() 臺,(假設(shè)可按產(chǎn)量全部賣出)
臺,(假設(shè)可按產(chǎn)量全部賣出)
(1)試用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 和
和![]() ;
;
(2)問新家電總產(chǎn)量超過多少臺時,該公司開始盈利?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com