
【題目】如圖,在平面直角坐標系中,已知拋物線y=ax2+bx﹣2(a≠0)與x軸交于A(1,0),B(3,0)兩點,與y軸交于點C,其頂點為點D,點E的坐標為(0,﹣1),該拋物線與BE交于另一點F,連接BC.
(1)求該拋物線的解析式;
(2)一動點M從點D出發,以每秒1個單位的速度沿與y軸平行的方向向上運動,連接OM,BM,設運動時間為t秒(t>0),在點M的運動過程中,當t為何值時,∠OMB=90°?
(3)在x軸上方的拋物線上,是否存在點P,使得∠PBF被BA平分?若存在,請直接寫出點P的坐標;若不存在,請說明理由.
【答案】
(1)
解:∵拋物線y=ax2+bx﹣2(a≠0)與x軸交于A(1,0)、B(3,0)兩點,
∴ ![]() ,
,
∴ 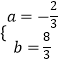 ,
,
∴拋物線解析式為y=﹣ ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
(2)
解:如圖1,
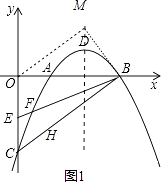
由(1)知y=﹣ ![]() x2+
x2+ ![]() x﹣2=﹣
x﹣2=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() ;
;
∵D為拋物線的頂點,
∴D(2, ![]() ),
),
∵一動點M從點D出發,以每秒1個單位的速度平沿行與y軸方向向上運動,
∴設M(2,m),(m> ![]() ),
),
∴OM2=m2+4,BM2=m2+1,OB2=9,
∵∠OMB=90°,
∴OM2+BM2=OB2,
∴m2+4+m2+1=9,
∴m= ![]() 或m=﹣
或m=﹣ ![]() (舍),
(舍),
∴M(0, ![]() ),
),
∴MD= ![]() ﹣
﹣ ![]() ,
,
∵一動點M從點D出發,以每秒1個單位的速度平沿行與y軸方向向上運動,
∴t= ![]() ﹣
﹣ ![]() ;
;
(3)
解:存在點P,使∠PBF被BA平分,
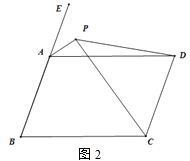
如圖2,
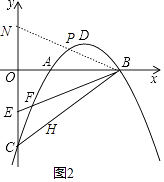
∴∠PBO=∠EBO,
∵E(0,﹣1),
∴在y軸上取一點N(0,1),
∵B(3,0),
∴直線BN的解析式為y=﹣ ![]() x+1①,
x+1①,
∵點P在拋物線y=﹣ ![]() x2+
x2+ ![]() x﹣2②上,
x﹣2②上,
聯立①②得 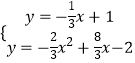 ,
,
解得 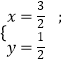 或
或 ![]() (舍去),
(舍去),
∴P( ![]() ,
, ![]() ).
).
【解析】(1)用待定系數法求出拋物線解析式;(2)設出點M,用勾股定理求出點M的坐標,從而求出MD,最后求出時間t;(3)由∠PBF被BA平分,確定出過點B的直線BN的解析式,求出此直線和拋物線的交點即可.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖①,E是直線AB,CD內部一點,AB∥CD,連接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,則∠AED= °
②猜想圖①中∠AED,∠EAB,∠EDC的關系,并用兩種不同的方法證明你的結論.
(2)拓展應用:
如圖②,射線FE與l1,l2交于分別交于點E、F,AB∥CD,a,b,c,d分別是被射線FE隔開的4個區域(不含邊界,其中區域a,b位于直線AB上方,P是位于以上四個區域上的點,猜想:∠PEB,∠PFC,∠EPF的關系(任寫出兩種,可直接寫答案).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】銷售有限公司到某汽車制造有限公司選購A、B兩種型號的轎車,用300萬元可購進A型轎車10輛,B型轎車15輛;用300萬元可購進A型轎車8輛,B型轎車18輛.
(1)求A、B兩種型號的轎車每輛分別多少元?
(2)若該汽車銷售公司銷售一輛A型轎車可獲利8000元,銷售一輛B型轎車可獲利5000元,該汽車銷售公司準備用不超過400萬元購進A、B兩種型號轎車共30輛,且這兩種轎車全部售出后總獲利不低于20.4萬元,問:有幾種購車方案?在這幾種購車方案中,哪種獲利最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組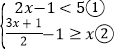
請結合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,C為線段BE上的一點,分別以BC和CE為邊在BE的同側作正方形ABCD和正方形CEFG,M、N分別是線段AF和GD的中點,連接MN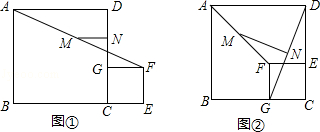
(1)線段MN和GD的數量關系是 , 位置關系是;
(2)將圖①中的正方形CEFG繞點C逆時針旋轉90°,其他條件不變,如圖②,(1)的結論是否成立?說明理由;
(3)已知BC=7,CE=3,將圖①中的正方形CEFG繞點C旋轉一周,其他條件不變,直接寫出MN的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,MN是⊙O的直徑,MN=4,∠AMN=40°,點B為弧AN的中點,點P是直徑MN上的一個動點,則PA+PB的最小值為( )
A.2
B.2 ![]()
C.2 ![]()
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小張同學學完統計知識后,隨機調查了她所在轄區若干名居民的年齡,將調查數據繪制成如下扇形統計圖和條形統計圖:

請根據以上不完整的統計圖提供的信息,解答下列問題:
(1)小張同學共調查了 名居民的年齡,扇形統計圖中a= ;
(2)補全條形統計圖,并注明人數;
(3)若該轄區年齡在0~14歲的居民約有3500人,請估計該轄區居民人數是多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
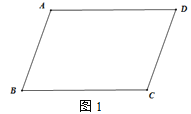
【題目】如圖1,已知AD∥BC,∠B=∠D.
(1)求證:AB∥CD;
(2)如圖2,點E為BA延長線上一點,∠EAD與∠BCD的角平分線交于點P.
①求∠APC的度數;
②連接DP,若∠PDC=750,則∠DPC-![]() ∠B=________.
∠B=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點P(x,y),我們把P’(y1,x1)叫做點P的友好點,已知點![]() 的友好點為
的友好點為![]() ,點
,點![]() 的友好點為
的友好點為![]() ,點
,點![]() 的友好點為
的友好點為![]() ,…,這樣依次得到點.
,…,這樣依次得到點.
(1)當點![]() 的坐標為(2,1),則點
的坐標為(2,1),則點![]() 的坐標為___,點
的坐標為___,點![]() 的坐標為___;
的坐標為___;
(2)若![]() 的坐標為(3,2),則設
的坐標為(3,2),則設![]() (x,y),求x+y的值;
(x,y),求x+y的值;
(3)設點A1的坐標為(a,b),若![]() ,
,![]() ,
,![]() ,…
,…![]() ,點
,點![]() 均在y軸左側,求a、b的取值范圍.
均在y軸左側,求a、b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com