
【題目】已知二次函數![]() .
.
(1)證明:不論![]() 取何值,該函數圖像與
取何值,該函數圖像與![]() 軸總有公共點;
軸總有公共點;
(2)若該函數的圖像與![]() 軸交于點(0,3),求出頂點坐標并畫出該函數圖像;
軸交于點(0,3),求出頂點坐標并畫出該函數圖像;
(3)在(2)的條件下,觀察圖像,解答下列問題:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有兩個不相等的實數根,則
有兩個不相等的實數根,則![]() 的取值范圍是 ;
的取值范圍是 ;
③若一元二次方程![]() 在
在![]() 的范圍內有實數根,則
的范圍內有實數根,則![]() 的取
的取
值范圍是 .
【答案】(1)證明見解析;(2)頂點(1,4);作圖略(3)①0<x<2;②k<4;③-5<t≤4
【解析】試題分析:(1)令y=0得到關于x的方程,找出相應的a,b及c的值,表示出![]() ,整理配方后,根據完全平方式大于等于0,判斷出
,整理配方后,根據完全平方式大于等于0,判斷出![]() 大于等于0,可得出拋物線與x軸總有交點,得證;
大于等于0,可得出拋物線與x軸總有交點,得證;
(2)由拋物線與y軸交于(0,3),將x=0,y=3代入拋物線解析式,求出m的值,進而確定出拋物線解析式,配方后找出頂點坐標,根據確定出的解析式列出相應的表格,由表格得出7個點的坐標,在平面直角坐標系中描出7個點,然后用平滑的曲線作出拋物線的圖象,如圖所示;
(3)由圖象和解析式即可可求得.
試題解析:(1) ![]()
∴不論m取何值,該函數圖象與x軸總有公共點,
(2)∵該函數的圖象與y軸交于點(0,3),
∴把x=0,y=3代入解析式得:m=3,
![]()
∴頂點坐標為(1,4);
列表如下:
x | 2 | 1 | 0 | 1 | 2 | 3 | 4 |
y | 5 | 0 | 3 | 4 | 3 | 0 | 5 |
描點;
畫圖如下:
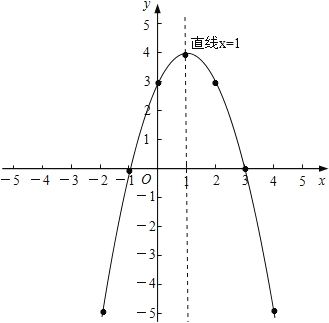
(3)根據圖象可知:①不等式![]() 的解集是:0<x<2,
的解集是:0<x<2,
②由拋物線的解析式![]() 可知若一元二次方程
可知若一元二次方程![]() 有兩個不相等的實數根,則k的取值范圍是:k<4,
有兩個不相等的實數根,則k的取值范圍是:k<4,
③若一元二次方程![]() 在1<x<4的范圍內有實數根,t的取值就是函數
在1<x<4的范圍內有實數根,t的取值就是函數![]() 在1<x<4的范圍內的函數值,由圖象可知在1<x<4的范圍內
在1<x<4的范圍內的函數值,由圖象可知在1<x<4的范圍內![]() ,故
,故![]()
故答案為0<x<2,k<4, ![]()


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:初中數學 來源: 題型:
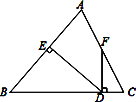
【題目】如圖所示,△ABC中,AB=BC,DE⊥AB于點E,DF⊥BC于點D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度數;
⑵若點F是AC的中點,求證:∠CFD=![]() ∠B.
∠B.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在防疫新冠狀病毒期間,市民對醫用口罩的需求越來越大.某藥店第一次用2000元購進醫用口罩若干個,第二次又用2000元購進該款口罩,但第二次每個口罩的進價是第一次進價的1.25倍,購進的數量比第一次少200個.
⑴求第一次和第二次分別購進的醫用口罩數量為多少個?
⑵藥店第一次購進口罩后,先以每個3元的價格出售,賣出了a個后購進第二批同款罩,由于進價提高了,藥店將口罩的售價也提升至每個3.5元繼續銷售賣出了b個后,兩次共收入4800元.因當地醫院醫療物資緊缺,藥店決定將剩余的口罩全部捐贈給醫院.請問藥店捐贈口罩至少有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料
在數軸上4與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]()
在數軸上![]() 與3所對的兩點之間的距離
與3所對的兩點之間的距離![]() ;
;
在數軸上![]() 與
與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]() 在數軸上點A、B分別表示數a、b,則A、B兩點之間的距離
在數軸上點A、B分別表示數a、b,則A、B兩點之間的距離![]()
依據材料知識解答下列問題
![]() 數軸上表示
數軸上表示![]() 和
和![]() 的兩點之間的距離是______,數軸上表示數x和3的兩點之間的距離表示為______;
的兩點之間的距離是______,數軸上表示數x和3的兩點之間的距離表示為______;
![]() 七年級研究性學習小組進行如下探究:
七年級研究性學習小組進行如下探究:
![]() 請你在草稿紙上面出數軸當表示數x的點在
請你在草稿紙上面出數軸當表示數x的點在![]() 與2之間移動時,
與2之間移動時,![]() 的值總是一個固定的值為:______,式子
的值總是一個固定的值為:______,式子![]() 的最小值是______.
的最小值是______.
![]() 請你在草稿紙上畫出數軸,當x等于______時,
請你在草稿紙上畫出數軸,當x等于______時,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A,B,C,D為矩形的四個頂點,AB=16 cm,AD=6 cm,動點P,Q分別從點A,C同時出發,點P以3 cm/s的速度向點B移動,一直到點B為止,點Q以2 cm/s的速度向點D移動,當點P停止運動時,點Q也停止運動.問:
(1)P,Q兩點從開始出發多長時間時,四邊形PBCQ的面積是33 cm2?
(2)P,Q兩點從開始出發多長時間時,點P與點Q之間的距離是10 cm?

查看答案和解析>>
科目:初中數學 來源: 題型:
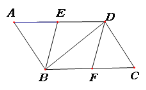
【題目】如圖,在平行四邊形ABCD中,點E、F分別是AD、BC的中點,分別連接BE、DF、BD.
(1)求證:△AEB≌△CFD;
(2)當△ABD滿足什么條件時,四邊形EBFD是菱形,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
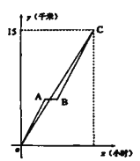
【題目】如圖,甲,乙兩人從點0出發去C地,甲的速度是乙速度的1.2倍,且甲在途中休息了半小時后仍按原速度行進.
(1)求甲,乙兩人的行進速度.
(2)求線段BC的解析式,并寫出定義域.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩江新區某小學每年的六一兒童節都會舉辦不同主題色的童裝盛會,記錄孩子們成長的印記這種活動讓商家們看到了新的商機,某網店獲悉今年的主題色是夢幻紫色,在六一節前購進夢幻紫色系列的A、B兩款童裝共86件,其中A款童裝120元每件.B款童裝80元每件,共用去資金8480元.
(1)求此網店購A、B兩款童裝各多少件?
(2)六一兒童節的童裝盛會反響非常好,引起社會上的童爸童媽們的高度關注,將這兩款童裝再次推向了熱銷,此網店決定再次購進A、B兩款童裝,數量與上次相同,購進時,發現A款童裝的進價上漲了![]() %,B款童裝的進價下降了之
%,B款童裝的進價下降了之![]() %,總價不超過9050元,求
%,總價不超過9050元,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com