
【題目】如圖,一次函數y=﹣ ![]() x+m(m>0)的圖象與x軸、y軸分別交于點A,B,點C在線段OA上,點C的橫坐標為n,點D在線段AB上,且AD=2BD,將△ACD繞點D旋轉180°后得到△A1C1D.
x+m(m>0)的圖象與x軸、y軸分別交于點A,B,點C在線段OA上,點C的橫坐標為n,點D在線段AB上,且AD=2BD,將△ACD繞點D旋轉180°后得到△A1C1D.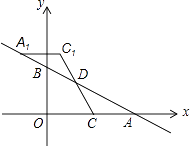
(1)若點C1恰好落在y軸上,試求 ![]() 的值;
的值;
(2)當n=4時,若△A1C1D被y軸分得兩部分圖形的面積比為3:5,求該一次函數的解析式.
【答案】
(1)解:由題意,得B(0,m),A(2m,0),
如圖,過點D作x軸的垂線,交x軸于點E,交直線A1C1于點F,
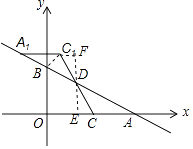
易知:DE= ![]() m,D(
m,D( ![]() m,
m, ![]() m),C1(
m),C1( ![]() m﹣n,
m﹣n, ![]() m),
m),
∴ ![]() m﹣n=0,∴
m﹣n=0,∴ ![]() =
= ![]()
(2)解:由(1)得,當m>3時,點C1在y軸右側;當2<m<3時,點C1在y軸左側.
①當m>3時,設A1C1與y軸交于點P,連接C1B,
由△A1C1D被y軸分得兩部分圖形的面積比為3:5,∴S△BA1P:S△BC1P=3:1,
∴A1P:C1P=3,∴ ![]() m=3(
m=3( ![]() m﹣4),∴m=
m﹣4),∴m= ![]() ,
,
∴y=﹣ ![]() x+
x+ ![]() ;
;
②當2<m<3時,同理可得:y=﹣ ![]() x+
x+ ![]() ;
;
綜上所述,y=﹣ ![]() x+
x+ ![]() 或y=﹣
或y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)由旋轉的性質可得AC1=AC,AD=A1D,當C1落在y軸上時,可得相似,即![]() ,對應邊成比例,得出AC1=
,對應邊成比例,得出AC1=![]() n,即2m-n=
n,即2m-n=![]() m,得出
m,得出![]() ;(2)可分類討論,m>3時,C1在y軸右側,可得出S△BA1P:S△BC1P=3:1,底邊長比也為3:1,進而求出解析式;當2<m<3時,點C1在y軸左側,類似的可求出解析式.
;(2)可分類討論,m>3時,C1在y軸右側,可得出S△BA1P:S△BC1P=3:1,底邊長比也為3:1,進而求出解析式;當2<m<3時,點C1在y軸左側,類似的可求出解析式.
【考點精析】關于本題考查的確定一次函數的表達式和旋轉的性質,需要了解確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法;①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了才能得出正確答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】綜合題
(1)如圖1,AC和BD相交于點O,OA=OC,OB=OD,求證:DC∥AB.
(2)如圖2,在⊙O中,直徑AB=6,AB與弦CD相交于點E,連接AC、BD,若AC=2,求cosD的值.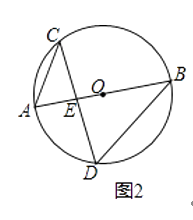
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點P是AB的中點,![]() 的延長線于點E,連接AE,過點A作
的延長線于點E,連接AE,過點A作![]() 交DP于點F,連接BF、
交DP于點F,連接BF、![]() 下列結論中:
下列結論中:![]() ≌
≌![]() ;
;![]() ;
;![]() 是等邊三角形;
是等邊三角形;![]() ;
;![]() 其中正確的是
其中正確的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】類比學習:
一動點沿著數軸向右平移![]() 個單位,再向左平移
個單位,再向左平移![]() 個單位,相當于向右平移
個單位,相當于向右平移![]() 個單位.用有理數加法表示為
個單位.用有理數加法表示為![]() .若坐標平面上的點做如下平移:沿
.若坐標平面上的點做如下平移:沿![]() 軸方向平移的數量為
軸方向平移的數量為![]() (向右為正,向左為負,平移
(向右為正,向左為負,平移![]() 個單位),沿
個單位),沿![]() 軸方向平移的數量為
軸方向平移的數量為![]() (向上為正,向下為負,平移
(向上為正,向下為負,平移![]() 個單位),則把有序數對
個單位),則把有序數對![]() 叫做這一平移的“平移量”;“平移量”
叫做這一平移的“平移量”;“平移量”![]() 與“平移量”
與“平移量”![]() 的加法運算法則為
的加法運算法則為![]()
解決問題:
(1)計算:![]() ;
;
(2)動點![]() 從坐標原點
從坐標原點![]() 出發,先按照“平移量”
出發,先按照“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移到
平移到![]() :若先把動點
:若先把動點![]() 按照.“平移量”
按照.“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移,最后的位置還是
平移,最后的位置還是![]() 嗎?在圖1中畫出四邊形
嗎?在圖1中畫出四邊形![]() .
.
(3)如圖2,一艘船從碼頭![]() 出發,先航行到湖心島碼頭
出發,先航行到湖心島碼頭![]() ,再從碼頭
,再從碼頭![]() 航行到碼頭
航行到碼頭![]() ,最后回到出發點
,最后回到出發點![]() .請用“平移量”加法算式表示它的航行過程.
.請用“平移量”加法算式表示它的航行過程.


解:(1)![]() ______;
______;
(2)答:______;
(3)加法算式:______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算或化簡:
(1)2﹣1+![]()
(2)2x2y(﹣3xy)÷(xy)2
(3)(﹣2a)(3a2﹣a+3)
(4)(x+3)(x+4)﹣(x﹣1)2
(5)[2a3x2(a﹣2x)﹣![]() a2x2]÷(﹣ax)2
a2x2]÷(﹣ax)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,購買“黃金1號”王米種子,所付款金額y元與購買量x(千克)之間的函數圖象由線段OA和射線AB組成,則購買1千克“黃金1號”玉米種子需付款___元,購買4千克“黃金1號”玉米種子需___元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(1,a),將線段OA平移至線段BC,B(b,0),a是m+6n的算術平方根,![]() =3,n=
=3,n=![]() ,且m<n,正數b滿足(b+1)2=16.
,且m<n,正數b滿足(b+1)2=16.
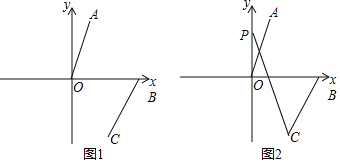
(1)直接寫出A、B兩點坐標為:A ,B ;
(2)如圖1,連接AB、OC,求四邊形AOCB的面積;
(3)如圖2,若∠AOB=a,點P為y軸正半軸上一動點,試探究∠CPO與∠BCP之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.
(1)、求證:四邊形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四邊形AODE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(2,0),點B(1,3).
(1)畫出將△OAB繞原點順時針旋轉90°后所得的△OA1B1,并寫出點A1,B1的坐標;
(2)畫出△OAB關于原點O的中心對稱圖形△OA2B2,并寫出點A2,B2的坐標.
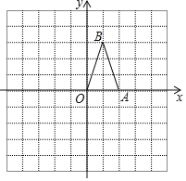
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com