
【題目】在平面直角坐標系中,點![]() 的坐標滿足:
的坐標滿足:![]()
(1)求出點![]() 的坐標
的坐標
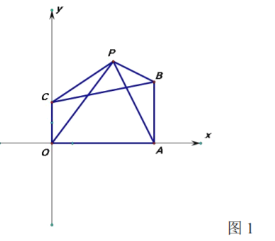
(2)如圖1,連接![]() ,點
,點![]() 在四邊形
在四邊形![]() 外面且在第一象限,再連
外面且在第一象限,再連![]() ,則
,則![]() ,求
,求![]() 點坐標.
點坐標.
(3)如圖2所示,![]() 為線段
為線段![]() 上一動點,
上一動點,![]() (在
(在![]() 右側)為
右側)為![]() 上一動點,使
上一動點,使![]() 軸始終平分
軸始終平分![]() ,連
,連![]() 且
且![]() ,那么
,那么![]() 是否為定值?若為定值,請直接寫出定值,若不是,請簡單說明理由.
是否為定值?若為定值,請直接寫出定值,若不是,請簡單說明理由.

【答案】(1)A(5,0),C(0,2);(2)P(3, ![]() );(3)
);(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.
【解析】
(1)根據絕對值和平方具有非負性得到2a-5c=0,c-2=0,解之即可得到a,c的值,從而得到A,C坐標;
(2)過P作PM⊥y軸,PN⊥AB的延長線,PH⊥x軸,因為![]() ,所以可得2PM=3PN,由圖知PM+PN=5,可得PM=3,PN=2,由
,所以可得2PM=3PN,由圖知PM+PN=5,可得PM=3,PN=2,由![]() 得
得![]() ,即
,即![]() ,可求出PH的值,從而得到P點坐標;
,可求出PH的值,從而得到P點坐標;
(3)設∠CDF=![]() ,OE與DF的交點為M,由四邊形內角和為360°,可得∠OMD的度數,根據三角形內角和為180°可得∠DEO的度數,根據已知可得∠DEF,而∠F=180°-∠DEF-∠FDE,將值代入即可求出∠F的度數.
,OE與DF的交點為M,由四邊形內角和為360°,可得∠OMD的度數,根據三角形內角和為180°可得∠DEO的度數,根據已知可得∠DEF,而∠F=180°-∠DEF-∠FDE,將值代入即可求出∠F的度數.
解:(1)∵![]()
∴![]()
解得![]()
∴A(5,0),C(0,2)
(2)過P作PM⊥y軸,PN⊥AB的延長線,PH⊥x軸

由(1)知A(5,0),C(0,2),B(5,3)
∵![]()
∴![]() CO
CO![]() PM=
PM=![]() AB
AB![]() PN
PN
∴![]() ×2PM=
×2PM=![]() ×3PN
×3PN
∴2PM=3PN
∵PM+PN=5
∴PM=3,PN=2
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
∴PH=![]()
∴P(3, ![]() )
)
(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.
設∠CDF=![]()
∴∠FDE=180°-2![]()
設OE與DF的交點為M

∴∠OMD=360°-![]() -
-![]() -90°=270°-
-90°=270°-![]() -
-![]()
∴∠DEO=∠OMD-∠FDE=90°+![]() -
-![]()
∴∠DEF=2∠DEO=180°+2![]() -2
-2![]()
∴∠F=180°-∠DEF-∠FDE=2![]() -180°
-180°
故答案為(1)A(5,0),C(0,2);(2)P(3, ![]() );(3)
);(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】請你根據如圖所示的阿寶與仙鶴的對話,解答下列問題:
(1)仙鶴為什么說多邊形內角和的度數不可能是![]() ;
;
(2)若圖中仙鶴所提到的外角的度數為![]() ,請分別求仙鶴所畫的多邊形的內角和的度數與邊數.
,請分別求仙鶴所畫的多邊形的內角和的度數與邊數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠第一季度生產甲、乙兩種機器共450臺,改進生產技術后,計劃第二季度生產這兩種機器共520臺,其中甲種機器增產10%,乙種機器增產20%,該廠第一季度生產甲、乙兩種機器各多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個定點坐標分別為A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)請畫出△ABC關于y軸對稱的△A1B1C1;
(2)以原點O為位似中心,將△ABC放大為原來的2倍,得到△A2B2C2 , 畫出△A2B2C2 , 并直接寫出S ![]() :S
:S ![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四張正面分別標有數字2,1,﹣3,﹣4的不透明卡片,它們除數字外其余全部相同,現將它們背面朝上,洗勻后從四張卡片中隨機地摸取一張不放回,將該卡片上的數字記為m,再隨機地摸取一張,將卡片上的數字記為n.
(1)請畫出樹狀圖并寫出(m,n)所有可能的結果;
(2)求所選出的m,n能使一次函數y=mx+n的圖象經過第二、三、四象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上A點表示數a,B點示數b,C點表示數c,b是最小的正整數,且a、b滿足|a+2|+(c﹣7)2=0.

(1)a= ,b= ,c= ;
(2)若將數軸折疊,使得A點與C點重合,則點B與數 表示的點重合;
(3)點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和4個單位長度的速度向右運動,假設t秒鐘過后,若點A與點B之間的距離表示為AB,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC.則AB= ,AC= ,BC= .(用含t的代數式表示)
(4)請問:3BC﹣2AB的值是否隨著時間t的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D是△ABC邊BC上一點,AD=BD,且AD平分∠BAC.(1)若∠B=50°,求∠ADC的度數;(2)若∠C=30°,求∠ADC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.動點P從點A出發,沿AB向點B運動,動點Q從點B出發,沿BC向點C運動,如果動點P以2cm/s,Q以1cm/s的速度同時出發,設運動時間為t(s),解答下列問題:
(1)t為______時,△PBQ是等邊三角形?
(2)P,Q在運動過程中,△PBQ的形狀不斷發生變化,當t為何值時,△PBQ是直角三角形?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在以下說法中:①實數分為正有理數、![]() 、負有理數.②實數和數軸上的點一一對應. ③過直線外一點有且只有一條直線和已知直線垂直.④過一點有且只有一條直線和已知直線 平行.⑤假命題不是命題.⑥如果兩條直線都和第三條直線平行,那么這兩條直線也互相平 行.⑦若一個數的立方根和平方根相同,那么這個數只能是
、負有理數.②實數和數軸上的點一一對應. ③過直線外一點有且只有一條直線和已知直線垂直.④過一點有且只有一條直線和已知直線 平行.⑤假命題不是命題.⑥如果兩條直線都和第三條直線平行,那么這兩條直線也互相平 行.⑦若一個數的立方根和平方根相同,那么這個數只能是![]() . 其中說法正確的個數是( )
. 其中說法正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com