
【題目】如圖,正方形ABCD的邊長是2,∠DAC的平分線交DC于點E,若點P、Q分別是AD和AE上的動點,則DQ+PQ的最小值為 .

【答案】![]() .
.
【解析】
試題過D作AE的垂線交AE于F,交AC于D′,再過D′作D′P′⊥AD,由角平分線的性質可得出D′是D關于AE的對稱點,進而可知D′P′即為DQ+PQ的最小值.
作D關于AE的對稱點D′,再過D′作D′P′⊥AD于P′,

∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D關于AE的對稱點,AD′=AD=2,
∴D′P′即為DQ+PQ的最小值,
∵四邊形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]()
,即DQ+PQ的最小值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】無人機技術我國逐漸發展迅速,全球首款噸位級貨運無人機從設計到總裝在四川成都雙流區完成,現有兩架航拍無人機:1號無人機從海拔5米處出發,以1米/秒的速度上升。與此同時,2號無人機從海拔15米處出發,以0.5米/秒的速度上升(設無人機上升時間為![]() 秒)。
秒)。
(1)求出1號無人機所在位置的海拔![]() (米)與
(米)與![]() 之間的關系式和2號無人機所在位置的海拔
之間的關系式和2號無人機所在位置的海拔![]() (米)與
(米)與![]() 之間的關系式?
之間的關系式?
(2)在某一時刻兩架無人機能否位于同一高度?如果能,請求出無人機上升的時間與高度?如果不能,請說明理由.
(3)上升多少時間,兩架無人機所在位置的海拔相差5米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解八年級學生對![]() (科學)、
(科學)、![]() (技術)、
(技術)、![]() (工程)、
(工程)、![]() (藝術)、
(藝術)、![]() (數學)中哪一個領域最感興趣的情況,該校對八年級學生進行了抽樣調查,根據調查結果繪制成如下的條形圖和扇形圖,請根據圖中提供的信息,解答下列問題:
(數學)中哪一個領域最感興趣的情況,該校對八年級學生進行了抽樣調查,根據調查結果繪制成如下的條形圖和扇形圖,請根據圖中提供的信息,解答下列問題:

(1)這次抽樣調查共調查了多少名學生?
(2)補全條形統計圖;
(3)求扇形統計圖中![]() (數學)所對應的圓心角度數;
(數學)所對應的圓心角度數;
(4)若該校八年級學生共有400人,請根據樣本數據估計該校八年級學生中對![]() (科學)最感興趣的學生大約有多少人?
(科學)最感興趣的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
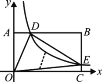
【題目】如圖,在以O為原點的直角坐標系中,矩形OABC的兩邊OC、OA分別在x軸、y軸的正半軸上,反比例函數![]() (x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k的值是( )
(x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC為邊作△ACE,∠ACE
2,以AC為邊作△ACE,∠ACE![]() 90°,AC=CE,延長BC至點D,使CD
90°,AC=CE,延長BC至點D,使CD![]() 5,連接DE.求證:△ABC∽△CED.
5,連接DE.求證:△ABC∽△CED.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)該二次函數圖象的對稱軸是x![]() ;
;
(2)若該二次函數的圖象開口向下,當![]() 時,
時, ![]() 的最大值是2,求當
的最大值是2,求當![]() 時,
時, ![]() 的最小值;
的最小值;
(3)若對于該拋物線上的兩點![]() ,
, ![]() ,當
,當![]() ,
, ![]() 時,均滿足
時,均滿足![]() ,請結合圖象,直接寫出
,請結合圖象,直接寫出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖AO和BD相交于點O,E是CD上一點,F是OD上一點,EF∥OC,∠1=∠A
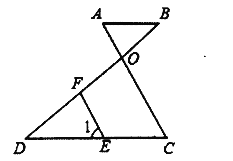
(1)試判斷AB和CD的位置關系,并說明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com