
【題目】將不等式組![]() 的解集在數(shù)軸上表示出來,正確的是( )
的解集在數(shù)軸上表示出來,正確的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
解一元一次不等式組,先求出不等式組中每一個不等式的解集,再利用口訣求出這些解集的公共部分:同大取大,同小取小,大小小大中間找,大大小小解不了(無解). 因此,
![]() ,由①得,
,由①得,![]() >3;由②得,
>3;由②得,![]() ≤4
≤4
∴其解集為:3<![]() ≤4
≤4
不等式組的解集在數(shù)軸上表示的方法:把每個不等式的解集在數(shù)軸上表示出來(>,≥向右畫;<,≤向左畫),數(shù)軸上的點(diǎn)把數(shù)軸分成若干段,如果數(shù)軸的某一段上面表示解集的線的條數(shù)與不等式的個數(shù)一樣,那么這段就是不等式組的解集.有幾個就要幾個。在表示解集時“≥”,“≤”要用實(shí)心圓點(diǎn)表示;“<”,“>”要用空心圓點(diǎn)表示. 因此,3<![]() ≤4在數(shù)軸上表示為:
≤4在數(shù)軸上表示為:
![]() , 故選C.
, 故選C.


 第三學(xué)期贏在暑假系列答案
第三學(xué)期贏在暑假系列答案 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案 浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
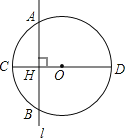
【題目】如圖,⊙O的半徑OC=10cm,直線l⊥CO,垂足為H,交⊙O于A,B兩點(diǎn),AB=16cm,直線l平移多少厘米時能與⊙O相切?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】先閱讀下面的內(nèi)容,再解決問題:
例題:若![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() +
+![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() (
(![]() )
)![]() +(
+(![]() -
-![]() )
)![]() =
=![]()
![]() -
-![]() =
=![]()
![]() -
-![]() ,
,![]()
問題:(1)若![]() -
-![]() -
-![]() =
=![]() , 求
, 求![]() 的值;
的值;
(2)已知![]() 的三邊長
的三邊長![]() 都是正整數(shù),且滿足
都是正整數(shù),且滿足![]() -
-![]() -
-![]() +
+![]() │3-
│3-![]() │=
│=![]() ,請問
,請問![]() 是怎樣形狀的三角形.
是怎樣形狀的三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】市教育局決定分別配發(fā)給一中8臺電腦,二中10臺電腦,但現(xiàn)在僅有12臺,需
在商場購買6臺. 從市教育局運(yùn)一臺電腦到一中、二中的運(yùn)費(fèi)分別是30元和50元,從商場
運(yùn)一臺電腦到一中、二中的運(yùn)費(fèi)分別是40元和80元. 要求總運(yùn)費(fèi)不超過840元,問有幾
種調(diào)運(yùn)方案?指出運(yùn)費(fèi)最低的方案。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】①已知:△ABC中,BC=m,∠A=60°.問滿足此條件的三角形有多少個?它們的最大面積存在嗎?若存在求出最大面積,并回答此時三角形的形狀;若不存在,請說明理由.

②有一個正方形的養(yǎng)魚塘,四個角各有一棵大樹.生產(chǎn)隊(duì)設(shè)想把魚塘擴(kuò)大,使它成為一個面積最大的正方形,而又不把樹挖掉,這一設(shè)想能否實(shí)現(xiàn)?若能,請你設(shè)計畫出圖形,并證明此時面積最大.若不能,請說明理由.

③上問題推廣,有一個正五邊形的養(yǎng)魚塘,五個角各有一棵樹,要擴(kuò)大使它成為面積最大的正五邊形,而又不把樹挖掉,可以嗎?畫圖說明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知ABC中∠A=60°,AB=2cm,AC=6cm,點(diǎn)P、Q分別是邊AB、AC上的動點(diǎn),點(diǎn)P從頂點(diǎn)A沿AB以1cm/s的速度向點(diǎn)B運(yùn)動,同時點(diǎn)Q從頂點(diǎn)C沿CA以3cm/s的速度向點(diǎn)A運(yùn)動,當(dāng)點(diǎn)P到達(dá)點(diǎn)B時點(diǎn)P、Q都停止運(yùn)動.設(shè)運(yùn)動的時間為t秒.

(1)當(dāng)t為何值時AP=AQ;
(2)是否存在某一時刻使得△APQ是直角三角形,若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CD⊥AB于點(diǎn)D,∠ACD=3∠BCD,E是斜邊AB的中點(diǎn),則∠ECD的度數(shù)為__________度.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,BD是邊長為1的正方形ABCD的對角線,BE平分∠DBC交DC于點(diǎn)E,延長BC到點(diǎn)F,使CF=CE,連接DF,交BE的延長線于點(diǎn)G.
(1)求證:△BCE≌△DCF;
(2)求CF的長。

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD的邊長是2,∠DAC的平分線交DC于點(diǎn)E,若點(diǎn)P、Q分別是AD和AE上的動點(diǎn),則DQ+PQ的最小值為 .

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com