Question

【題目】如圖，⊙O的內接四邊形ABCD兩組對邊的延長線分別交于點E、F．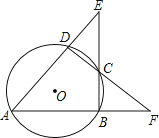

（1）若∠E=∠F時，求證：∠ADC=∠ABC；
（2）（2）若∠E=∠F=42°時，求∠A的度數
（3）（3）若∠E=α，∠F=β，且α≠β．請你用含有α、β的代數式表示∠A的大小．

Answer 1

【答案】
（1）

（1）∠E=∠F，

∵∠DCE=∠BCF，

∴∠ADC=∠E+∠DCE，∠ABC=∠F+∠BCF，

∴∠ADC=∠ABC；

（2）

（2）由（1）知∠ADC=∠ABC，

∵∠EDC=∠ABC，

∴∠EDC=∠ADC，

∴∠ADC=90°，

∴∠A=90°﹣42°=48°；

（3）

（3）連結EF，如圖，

∵四邊形ABCD為圓的內接四邊形，

∴∠ECD=∠A，

∵∠ECD=∠1+∠2，

∴∠A=∠1+∠2，

∵∠A+∠1+∠2+∠E+∠F=180°，

∴2∠A+α+β=180°，

∴∠A=90°﹣．

【解析】（1）根據外角的性質即可得到結論；
（2）根據圓內接四邊形的性質和等量代換即可求得結果；
（3）連結EF，如圖，根據圓內接四邊形的性質得∠ECD=∠A，再根據三角形外角性質得∠ECD=∠1+∠2，則∠A=∠1+∠2，然后根據三角形內角和定理有∠A+∠1+∠2+∠E+∠F=180°，即2∠A+α+β=180°，再解方程即可．