
【題目】在![]() 中,已知
中,已知![]() ,
,![]() 為
為![]() 的角平分線.\
的角平分線.\
(1)如圖1,當![]() 時,在
時,在![]() 邊上截取
邊上截取![]() ,連接
,連接![]() ,你能發(fā)現線段
,你能發(fā)現線段![]() 、
、![]() 、
、![]() 之間有怎樣的數量關系么?請直接寫出你的發(fā)現:________________________(不需要證明);
之間有怎樣的數量關系么?請直接寫出你的發(fā)現:________________________(不需要證明);

(2)如圖2,當![]() 時,線段
時,線段![]() 、
、![]() 、
、![]() 還有(1)中的數量關系么?請證明你的猜想;
還有(1)中的數量關系么?請證明你的猜想;
(3)如圖3,當![]() 為
為![]() 的外角平分線時,線段
的外角平分線時,線段![]() 、
、![]() 、
、![]() 又有怎樣的數量關系?不需要證明,請直接寫出你的猜想:______________________.
又有怎樣的數量關系?不需要證明,請直接寫出你的猜想:______________________.
【答案】(1)AB=AC+CD,理由見解析;(2)還成立,理由見解析;(3)AB+AC=CD,理由見解析;
【解析】
(1)由AD為∠BAC的角平分線,得到∠EAD=∠CAD,通過△AED≌△ACD,得到ED=CD,∠AED=∠ACD=90°,由于∠ACB=90°,∠ACB=2∠B,得到∠B=45°,∠BDE=45°,∠B=∠BDE,根據等腰三角形的性質得到EB=ED,于是得到結論;
(2)如圖2,在AB上截取AE=AC,連接ED,由AD為∠BAC的角平分線時,得到∠BAD=∠CAD,通過△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根據等腰三角形的性質得到EB=ED,即可得解;
(3)如圖3,在BA的延長線上截取AE=AC,連接ED,由AD為∠BAC的角平分線時,得到∠BAD=∠CAD,通過△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根據等腰三角形的性質得到EB=ED,即可得解.
證明:(1)AB=AC+CD
理由如下:
∵AD為∠BAC的角平分線

∴∠EAD=∠CAD,
在△AED與△ACD中,
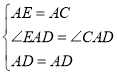
∴△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠ACD=90°,
又∵∠ACB=90°,∠ACB=2∠B,
∴∠B=45°,
∴∠BDE=45°,
∴∠B=∠BDE,
∴EB=ED,
∴EB=CD,
∴AB=AE+EB=AC+CD;
故答案為:AB=AC+CD
(2)結論:還成立.
理由:如圖2,在AB上截取AE=AC,連接ED,
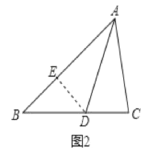
∵AD為∠BAC的角平分線時,
∴∠BAD=∠CAD,
在△AED與△ACD中,
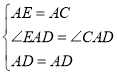
∴△AED≌△ACD(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+EB=AC+CD;
(3)猜想:AB+AC=CD.
證明:如圖3,在BA的延長線上截取AE=AC,連接ED.
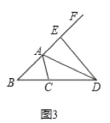
∵AD平分∠FAC,
∴∠EAD=∠CAD,
在△AED與△ACD中,
∴△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠ACD,
∴∠FED=∠ACB,
又∵∠ACB=2∠B,
∴∠FED=2∠B,
又∵∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴EB=ED,
∴EA+AB=EB=ED=CD,
∴AC+AB=CD.


科目:初中數學 來源: 題型:
【題目】如圖,數軸上A,B兩點對應的有理數分別為xA=﹣5和xB=6,動點P從點A出發(fā),以每秒1個單位的速度沿數軸在A,B之間往返運動,同時動點Q從點B出發(fā),以每秒2個單位的速度沿數軸在B,A之間往返運動.設運動時間為t秒.
(1)當t=2時,點P對應的有理數xP=______,PQ=______;
(2)當0<t≤11時,若原點O恰好是線段PQ的中點,求t的值;
(3)我們把數軸上的整數對應的點稱為“整點”,當P,Q兩點第一次在整點處重合時,直接寫出此整點對應的數.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店用4500元購進一批襯衫,很快售完,服裝店老板又用2100元購進第二批該款式的襯衫,進貨量是第一次的一半,但進價每件比第一批降低了10元.
(1)這兩次各購進這種襯衫多少件?
(2)若第一批襯衫的售價是200元/件,老板想讓這兩批襯衫售完后的總利潤不低于2100元,則第二批襯衫每件至少要售多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:我們知道![]() 的幾何意義是在數軸上數
的幾何意義是在數軸上數![]() 對應的點與原點的距離,即
對應的點與原點的距離,即![]() ,也就是說,
,也就是說,![]() 表示在數軸上數
表示在數軸上數![]() 與數
與數![]() 對應點之間的距離.這個結論可以推廣為:
對應點之間的距離.這個結論可以推廣為:![]() 表示在數軸上數
表示在數軸上數![]() 與
與![]() 對應點之間的距離.
對應點之間的距離.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在數軸上與原點距離為![]() 的點的對應數為
的點的對應數為![]() 和
和![]() ,即
,即![]() 的值為
的值為![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在數軸上與![]() 的距離為
的距離為![]() 點的對應數為
點的對應數為![]() 和
和![]() ,即
,即![]() 的值為
的值為![]() 和
和![]() .
.
仿照閱讀材料的解法,解決下列問題:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若數軸上表示![]() 的點在
的點在![]() 與
與![]() 之間,則
之間,則![]() 的值為_________;
的值為_________;
(4)當![]() 滿足_________時,則
滿足_________時,則![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
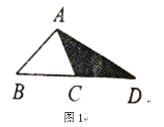
【題目】閱讀理解,并完成填空:在圖1至圖3中,己知![]() 的面積為
的面積為![]() .
.
(1)如圖1,延長![]() C的邊
C的邊![]() 到點
到點![]() ,使
,使![]() ,連結
,連結![]() .若
.若![]() 的面積為
的面積為![]() ,則
,則![]() __________(用含
__________(用含![]() 的代數式表示);
的代數式表示);
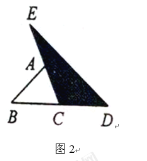
(2)如圖2,延長![]() 的邊
的邊![]() 到點
到點![]() ,延長邊
,延長邊![]() 到點
到點![]() ,使
,使![]() ,
,![]() ,連結
,連結![]() ,若
,若![]() 的面積為
的面積為![]() ,則
,則![]() __________(用含
__________(用含![]() 的代數式表示);
的代數式表示);
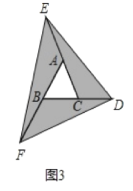
(3)在圖2的基礎上延長AB到點F,使BF=AB,連接FD,得到△DEF(如圖3),若陰影部分的面積為S3,則S3=___(用含a的代數式表示)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進甲、乙兩種商品,已知每件甲種商品的價格比每件乙種商品的價格貴10元,用350元購買甲種商品的件數恰好與用300元購買乙種商品的件數相同.
(1)求甲、乙兩種商品每件的價格各是多少元?
(2)計劃購買這兩種商品共50件,且投入的經費不超過3200元,那么,最多可購買多少件甲種商品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,給正五邊形的頂點依次編號為1,2,3,4,5.若從某一頂點開始,沿正五邊形的邊順時針方向行走,頂點編號的數字是幾,就走幾個邊長,則稱這種走法為一次“移位”.如:小宇在編號為3的頂點上時,那么他應走3個邊長,即從3→4→5→1為第一次“移位”,這時他到達編號為1的頂點;然后從1→2為第二次“移位”.若小宇從編號為2的頂點開始,第15次“移位”后,則他所處頂點的編號為__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩城間的鐵路路程為1600千米,經過技術改造,列車實施了提速,提速后比提速前速度增加了20千米/小時,列車從甲城到乙城行駛時間減少4小時,這條鐵路在現有條件下安全行駛速度不得超過140千米/小時,請你用學過的知識說明在這條鐵路的現有條件下列車是否還可以再提速。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為舉辦校園文化藝術節(jié),甲、乙兩班準備給合唱同學購買演出服裝(一人一套),兩班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供貨商給出的演出服裝的價格表:
購買服裝的套數 | 1套至45套 | 46套至90套 | 91套以上 |
每套服裝的價格 | 60元 | 50元 | 40元 |
如果兩班單獨給每位同學購買一套服裝,那么一共應付5020元.
(1)甲、乙兩班聯(lián)合起來給每位同學購買一套服裝,比單獨購買可以節(jié)省多少錢?
(2)甲、乙兩班各有多少名同學?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com