
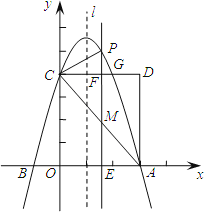
【題目】如圖,拋物線![]() (a≠0)交x軸于A、B兩點,A點坐標為(3,0),與y軸交于點C(0,4),以OC、OA為邊作矩形OADC交拋物線于點G.
(a≠0)交x軸于A、B兩點,A點坐標為(3,0),與y軸交于點C(0,4),以OC、OA為邊作矩形OADC交拋物線于點G.
(1)求拋物線的解析式;
(2)拋物線的對稱軸l在邊OA(不包括O、A兩點)上平行移動,分別交x軸于點E,交CD于點F,交AC于點M,交拋物線于點P,若點M的橫坐標為m,請用含m的代數式表示PM的長;
(3)在(2)的條件下,連結PC,則在CD上方的拋物線部分是否存在這樣的點P,使得以P、C、F為頂點的三角形和△AEM相似?若存在,求出此時m的值;若不存在,請說明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+4;(2)PM=-
x+4;(2)PM=-![]() m2+4m(0<m<3);(3)存在這樣的點P使△PFC與△AEM相似.此時m的值為
m2+4m(0<m<3);(3)存在這樣的點P使△PFC與△AEM相似.此時m的值為![]() 或1.
或1.
【解析】
試題分析:(1)將A(3,0),C(0,4)代入y=ax2-2ax+c,運用待定系數法即可求出拋物線的解析式;
(2)先根據A、C的坐標,用待定系數法求出直線AC的解析式,進而根據拋物線和直線AC的解析式分別表示出點P、點M的坐標,即可得到PM的長;
(3)由于∠PFC和∠AEM都是直角,F和E對應,則若以P、C、F為頂點的三角形和△AEM相似時,分兩種情況進行討論:①△PFC∽△AEM,②△CFP∽△AEM;可分別用含m的代數式表示出AE、EM、CF、PF的長,根據相似三角形對應邊的比相等列出比例式,求出m的值.
試題解析:(1)∵拋物線y=ax2-2ax+c(a≠0)經過點A(3,0),點C(0,4),
∴![]() ,
,
解得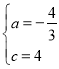 .
.
∴拋物線的解析式為y=-![]() x2+
x2+![]() x+4;
x+4;
(2)設直線AC的解析式為y=kx+b,
∵A(3,0),點C(0,4),
∴![]() ,
,
解得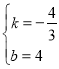 .
.
∴直線AC的解析式為y=-![]() x+4.
x+4.
∵點M的橫坐標為m,點M在AC上,
∴M點的坐標為(m,-![]() m+4),
m+4),
∵點P的橫坐標為m,點P在拋物線y=-![]() x2+
x2+![]() x+4上,
x+4上,
∴點P的坐標為(m,-![]() m2+
m2+![]() m+4),
m+4),
∴PM=PE-ME=(-![]() m2+
m2+![]() m+4)-(-
m+4)-(-![]() m+4)=-
m+4)=-![]() m2+4m,
m2+4m,
即PM=-![]() m2+4m(0<m<3);
m2+4m(0<m<3);
(3)在(2)的條件下,連結PC,在CD上方的拋物線部分存在這樣的點P,使得以P、C、F為頂點的三角形和△AEM相似.理由如下:由題意,可得AE=3-m,EM=-![]() m+4,CF=m,若以P、C、F為頂點的三角形和△AEM相似,情況:
m+4,CF=m,若以P、C、F為頂點的三角形和△AEM相似,情況:
①P點在CD上方,則PF=-![]() m2+
m2+![]() m+4-4=-
m+4-4=-![]() m2+
m2+![]() m.
m.
若△PFC∽△AEM,則PF:AE=FC:EM,
即(-![]() m2+
m2+![]() m):(3-m)=m:(-
m):(3-m)=m:(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=![]() ;
;
②若△CFP∽△AEM,則CF:AE=PF:EM,
即m:(3-m)=(-![]() m2+
m2+![]() m):(-
m):(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=1.
綜上所述,存在這樣的點P使△PFC與△AEM相似.此時m的值為![]() 或1.
或1.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】
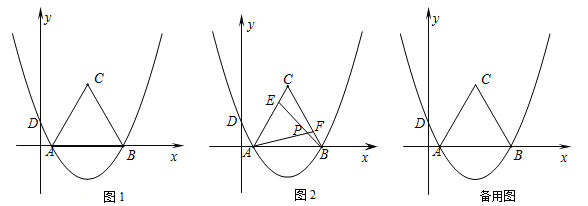
如圖1,拋物線經過A(1,0),B(7,0),D(0,![]() ) 三點,以AB為邊在x軸上方作等邊三角形ABC.
) 三點,以AB為邊在x軸上方作等邊三角形ABC.
(1)求拋物線的解析式;
(2)在拋物線x軸上方是否存在點M,使S△ABM =![]() S△ABC,若存在,請求出點M坐標;若不存在,請說明理由;
S△ABC,若存在,請求出點M坐標;若不存在,請說明理由;
(3)如圖2,E是線段AC上的動點,F是線段BC上的動點,AF與BE相交于點P.
①若CE=BF,試猜想AF與BE的數量關系,請說明理由,并求出∠APB的度數;
②若AF=BE,當點E由A運動到C時,試求點P經過的路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
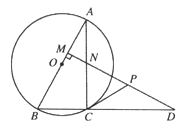
【題目】如圖所示,△ABC的外接圓圓心O在AB上,點D是BC延長線上一點,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的ND邊的中線.
(1)求證:△ABC≌△DNC;
(2)試判斷CP與⊙O的位置關系,并證明你的結論。
查看答案和解析>>
科目:初中數學 來源: 題型:
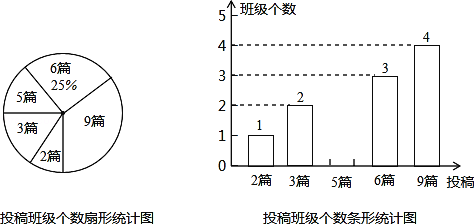
【題目】為積極響應市委,市政府提出的“實現偉大中國夢,建設美麗新城市”的號召,我市某校在八,九年級開展征文活動,校學生會對這兩個年級各班內的投稿情況進行統計,并制成了如圖所示的兩幅不完整的統計圖.
(1)求扇形統計圖中投稿篇數為2所對應的扇形的圓心角的度數:
(2)求該校八,九年級各班在這一周內投稿的平均篇數,并將該條形統計圖補充完整.
(3)在投稿篇數為9篇的兩個班級中,八,九年級各有兩個班,校學生會準備從這四個中選出兩個班參加全市的表彰會,請你用列表法或畫樹狀圖的方法求出所選兩個班正好不在同一年級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B的坐標分別為(1,1)和(5,4),拋物線y=ax2+bx+c(a≠0)的頂點在線段AB上運動,與x軸交于C、D兩點(C在D的左側),當拋物線的頂點為A時,點C的橫坐標為O,則點D的橫坐標最大值為( )

A.5 B.6 C.7 D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在東西方向的海岸線l上有一長為1千米的碼頭MN,在碼頭西端M的正西方向30 千米處有一觀察站O.某時刻測得一艘勻速直線航行的輪船位于O的北偏西30°方向,且與O相距20![]() 千米的A處;經過40分鐘,又測得該輪船位于O的正北方向,且與O相距20千米的B處.
千米的A處;經過40分鐘,又測得該輪船位于O的正北方向,且與O相距20千米的B處.
(1)求該輪船航行的速度;
(2)如果該輪船不改變航向繼續航行,那么輪船能否正好行至碼頭MN靠岸?請說明理由.(參考數據:![]() ,
,![]() )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com