
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,連接AC,∠MAC=∠CAB,作CD⊥AM,垂足為D. 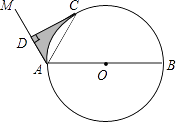
(1)求證:CD是⊙O的切線;
(2)若∠ACD=30°,AD=4,求圖中陰影部分的面積.
【答案】
(1)證明:連接OC.
∵OA=OC.
∴∠OAC=∠OCA,
∵∠MAC=∠OAC,
∴∠MAC=∠OCA,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∴CD是⊙O的切線

(2)解:在RT△ACD中,∵∠ACD=30°,AD=4,∠ADC=90°,
∴AC=2AD=8,CD= ![]() AD=4
AD=4 ![]() ,
,
∵∠MAC=∠OAC=60°,OA=OC,
∴△AOC是等邊三角形,
∴S陰=S△ACD﹣(S扇形OAC﹣S△AOC)
= ![]() ×4×4
×4×4 ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×82)
×82)
=24 ![]() ﹣
﹣ ![]() π
π
【解析】(1)先證明OC∥AM,由CD⊥AM,推出OC⊥CD即可解決問題.(2)根據S陰=S△ACD﹣(S扇形OAC﹣S△AOC)計算即可.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】在開展“好書伴我成長”的讀書活動中,某中學為了解八年級300名學生讀書情況,隨機調查了八年級50名學生讀書的冊數.統計數據如下表所示:

(1)求這50個樣本數據的平均救,眾數和中位數.
(2)根據樣本數據,估計該校八年級300名學生在本次活動中讀書多于2冊的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩組卡片共5張,A中三張分別寫有數字2,4,6,B中兩張分別寫有3,5.它們除了數字外沒有任何區別.
(1)隨機地從A中抽取一張,求抽到數字為2的概率;
(2)隨機地分別從A、B中各抽取一張,請你用畫樹狀圖或列表的方法表示所有等可能的結果,現制定這樣一個游戲規則:若選出的兩數之積為3的倍數,則甲獲勝;否則乙獲勝.請問這樣的游戲規則對甲乙雙方公平嗎?為什么?
(3)如果不公平請你修改游戲規則使游戲規則對甲乙雙方公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)已知關于x的方程kx=11﹣2x有整數解,則負整數k的值為 .
(2)若a+b+c=0,且a>b>c,以下結論:
①a>0,c>0;
②關于x的方程ax+b+c=0的解為x=1;
③a2=(b+c)2;
④![]() 的值為0或2;
的值為0或2;
⑤在數軸上點A、B、C表示數a、b、c,若b<0,則線段AB與線段BC的大小關系是AB>BC.
其中正確的結論是 (填寫正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1,3,6,10…這樣的數稱為“三角形數”,而把1,4,9,16…這樣的數稱為“正方形數”.從圖中可以發現,任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和.下列等式中,符合這一規律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形OABC的邊長為4,對角線相交于點P,拋物線L經過O、P、A三點,點E是正方形內的拋物線上的動點.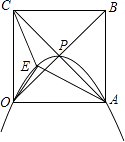
(1)建立適當的平面直角坐標系,
①直接寫出O、P、A三點坐標;
②求拋物線L的解析式;
(2)求△OAE與△OCE面積之和的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:問題:如圖1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,點A,B,E在同一條直線上,P是線段DF的中點,連接PG,PC,探究PG與PC的位置關系。
(1)請你寫出上面問題中線段PG與PC的位置關系,并說明理由;
(2)將圖1中的菱形BEFG繞點B順時針旋轉,使菱形BEFG的對角線BF恰好與菱形ABCD的邊AB在同一條直線上,原問題中的其他條件不變(如圖2).你在(1)中得到的結論是否發生變化?寫出你的猜想并加以證明,
(3)將菱形ABCD和菱形BEFG均改成正方形,如圖3,P為DF的中點,此時PG與PC的位置關系和數量關系分別是什么?直接寫出答案。



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把幾個數用大括號圍起來,中間用逗號斷開,如:{1,2,﹣3}、{﹣2,7,![]() ,19},我們稱之為集合,其中的每個數稱為該集合的元素.如果一個所有元素均為有理數的集合滿足:當有理數a是集合的元素時,2015﹣a也必是這個集合的元素,這樣的集合我們稱為好的集合.例如集合{2015,0}就是一個好的集合.
,19},我們稱之為集合,其中的每個數稱為該集合的元素.如果一個所有元素均為有理數的集合滿足:當有理數a是集合的元素時,2015﹣a也必是這個集合的元素,這樣的集合我們稱為好的集合.例如集合{2015,0}就是一個好的集合.
(1)集合{2015}_____好的集合,集合{﹣1,2016}_____好的集合(兩空均填“是”或“不是”);
(2)若一個好的集合中最大的一個元素為4011,則該集合是否存在最小的元素?如果存在,請直接寫出答案,否則說明理由;
(3)若一個好的集合所有元素之和為整數M,且22161<M<22170,則該集合共有幾個元素?說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上點A對應的數為![]() ,點B對應的數為
,點B對應的數為![]() ,且多項式
,且多項式![]() 的二次項系數為
的二次項系數為![]() ,常數項為
,常數項為![]() .
.
(1)直接寫出:![]() ;
;
(2)數軸上點A、B之間有一動點P,若點P對應的數為![]() ,試化簡
,試化簡![]() ;
;
(3)若點M從點A出發,以每秒1個單位長度的速度沿數軸向右移動;同時點N從點B出發,沿數軸每秒2個單位長度的速度向左移動,到達A點后立即返回并向右繼續移動,求經過多少秒后,M、N兩點相距1個單位長度?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com