
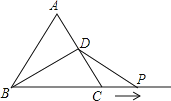
【題目】如圖,等邊△ABC的邊長為10cm,點D是邊AC的中點,動點P從點C出發,沿BC的延長線以2cm/s的速度做勻速運動,設點P的運動時間為t(秒),若△BDP是等腰三角形,求t的值.
科目:初中數學 來源: 題型:
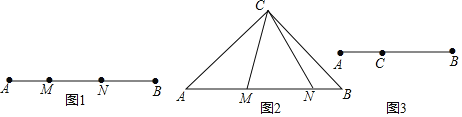
【題目】定義,如圖1,點M,N把線段AB分割成AM,MN和BN,若以AM,MN,BN為邊的三角形是一個直角三角形,則稱點M,N為線段AB的勾股分割點.
(1)已知點M,N是線段AB的勾股分割點,若AM=3,MN=5,求BN的長
(2)如圖2,在Rt△ABC中,AC=BC,點M,N在斜邊AB上,∠MCN=45°,求證:點M,N是線段AB的勾股分割點;陽陽在解決第(2)小題時遇到了困難,陳老師對陽陽說:要證明勾股分割點,則需設法構造直角三角形,你可以把△CBN繞點C逆時針旋轉90度試試,請根據陳老師的提示完成證明過程.
(3)如圖3,C是線段AB上的一定點,請在BC上畫一點D,使C、D是線段AB的勾股分割點
(要求:完成尺規作圖,保留作圖痕跡,并在右側分步寫出作圖步驟)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD內接于圓O,連結BD,∠BAD=105°,∠DBC=75°.
(1)求證:BD=CD;
(2)若圓O的半徑為3,求 ![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
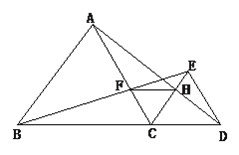
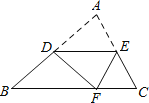
【題目】如圖,已知點B、C、D在同一條直線上,△ABC和△CDE都是等邊三角形.BE交AC于F,AD交CE于H,
①求證:△BCE≌△ACD;
②求證:CF=CH;
③判斷△CFH的形狀并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .點E為線段BD上任意一點(點E與點B,D不重合),過點E作EF∥CD,與BC相交于點F,連接CE.設BE=x,y=
.點E為線段BD上任意一點(點E與點B,D不重合),過點E作EF∥CD,與BC相交于點F,連接CE.設BE=x,y= ![]() .
.
(1)求BD的長;
(2)如果BC=BD,當△DCE是等腰三角形時,求x的值;
(3)如果BC=10,求y關于x的函數解析式,并寫出自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
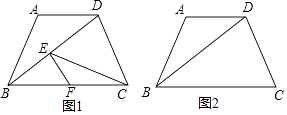
【題目】如圖1,在四邊形ABCD中,∠DAB被對角線AC平分,且AC2=ABAD.我們稱該四邊形為“可分四邊形”,∠DAB稱為“可分角”.
(1)如圖2,在四邊形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求證:四邊形ABCD為“可分四邊形”;
(2)如圖3,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,如果∠DCB=∠DAB,則求∠DAB的度數;
(3)現有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4,則△DAB的最大面積等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】看圖填空:

(1)∠1和∠3是直線________被直線____所截得的______;
(2)∠1和∠4是直線_________被直線____所截得的______;
(3)∠B和∠2是直線_________被直線_____所截得的______;
(4)∠B和∠4是直線_________被直線_____所截得的_______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=70°∠B=50°,點D,E分別為AB,AC上的點,沿DE折疊,使點A落在BC邊上點F處,若△EFC為直角三角形,則∠BDF的度數為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com