
【題目】拋物線y=ax2+bx+3(a≠0)過A(4,4),B(2,m)兩點,點B到拋物線對稱軸的距離記為d,滿足0<d≤1,則實數m的取值范圍是( )
A.m≤2或m≥3
B.m≤3或m≥4
C.2<m<3
D.3<m<4
【答案】B
【解析】解:把A(4,4)代入拋物線y=ax2+bx+3得: 16a+4b+3=4,
∴16a+4b=1,
∴4a+b= ![]() ,
,
∵對稱軸x=﹣ ![]() ,B(2,m),且點B到拋物線對稱軸的距離記為d,滿足0<d≤1,
,B(2,m),且點B到拋物線對稱軸的距離記為d,滿足0<d≤1,
∴ ![]()
∴ ![]() ,
,
∴| ![]() |≤1,
|≤1,
∴ ![]() 或a
或a ![]() ,
,
把B(2,m)代入y=ax2+bx+3得:
4a+2b+3=m
2(2a+b)+3=m
2(2a+ ![]() ﹣4a)+3=m
﹣4a)+3=m![]() ﹣4a=m,
﹣4a=m,
a= ![]() ,
,
∴ ![]() 或
或 ![]() ,
,
∴m≤3或m≥4.
故選:B.
【考點精析】認真審題,首先需要了解二次函數的性質(增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小).


科目:初中數學 來源: 題型:
【題目】如圖,某船以每小時36海里的速度向正東方向航行,在點A測得某島C在北偏東60°方向上,航行半小時后到達點B測得該島在北偏東30°方向上,已知該島周圍16海里內有暗礁.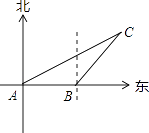
(1)說明點B是否在暗礁區域內;
(2)若繼續向東航行有無觸礁的危險?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩城相距600千米,一輛客車從A城開往B城,車速為每小時80千米,同時一輛出租車從B城開往A城,車速為毎小時100千米,設客車出時間為t. ![]()
(1)【探究】 若客車、出租車距B城的距離分別為y1、y2 , 寫出y1、y2關于t的函數關系式,并計算當y1=200千米時y2的値.
(2)【發現】 設點C是A城與B城的中點,
(Ⅰ)哪個車會先到達C?該車到達C后再經過多少小時,另一個車會到達C?
(Ⅱ)若兩車扣相距100千米時,求時間t.
(3)【決策】 己知客車和出租車正好在A,B之間的服務站D處相遇,此時出租車乘客小王突然接到開會通知,需要立即返回,此時小王有兩種選擇返回B城的方案:
方案一:繼續乘坐出租車,到達A城后立刻返回B城(設出租車調頭時間忽略不計);
方案二:乘坐客車返回城.
試通過計算,分析小王選擇哪種方式能更快到達B城?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國很多城市水資源缺乏,為了加強居民的節水意識,某市制定了每月用水4噸以內(包括4噸)和用水4噸以上兩種收費標準(收費標準:每噸水的價格),某用戶每月應交水費y(元)是用水量x(噸)的函數,其函數圖象如圖所示.
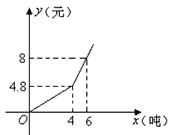
(1)分別求出當0≤x≤4、x>4時函數的解析式;
(2)當0≤x≤4、x>4時,每噸水的價格分別是多少?
(3)若某用戶該月交水費12.8元,求該戶用了多少噸水.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是△ABC的角平分線,DE∥BC,交AB于點E,DF∥AB,交BC于點F,當△ABC滿足_________條件時,四邊形BEDF是正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,正比例函數
中,正比例函數![]() 與反比例函數
與反比例函數![]() 的圖象交于A,B兩點,A點的橫坐標為2,AC⊥x軸于點C,連接BC.
的圖象交于A,B兩點,A點的橫坐標為2,AC⊥x軸于點C,連接BC.
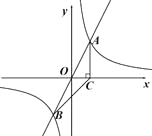
(1)求反比例函數的解析式;
(2)若點P是反比例函數![]() 圖象上的一點,且滿足△OPC與△ABC的面積相等,請直接寫出點P的坐標.
圖象上的一點,且滿足△OPC與△ABC的面積相等,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=1,BC=7,將矩形ABCD繞點C逆時針旋轉90°得到矩形A′B′CD′,點E、F分別是BD、B′D′的中點,則EF的長度為________cm.
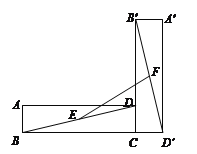
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com