
【題目】閱讀下列文字與例題,并解答。
將一個多項式分組進行因式分解后,可用提公因式法或公式法繼續分解的方法稱作分組分解法。例如:以下式子的分解因式的方法叉稱為分組分解法。
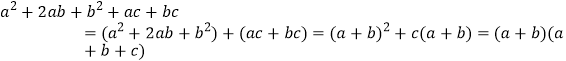 (1)試用“分組分解法”分解因式:
(1)試用“分組分解法”分解因式:![]()
(2)已知四個實數a,b,c,d滿足![]() 。并且
。并且![]() ,
,![]() ,
,![]() ,
,![]() 同時成立。
同時成立。
①當k=1時,求a+c的值;
②當k≠0時,用含a的代數式分別表示b、c、d。
【答案】(1)(x﹣y)(x+y+z);(2)①a+c=±6;②c=2a,b=d=﹣3a.
【解析】
(1)根據因式分解-分組分解法分解即可;
(2)根據因式分解-分組分解法和提公因式法分解即可.
解:(1)x2﹣y2+xz﹣yz=(x+y)(x﹣y)+z(x﹣y)
=(x﹣y)(x+y+z);
(2)①當k=1 時,得a2+ac=12,c2+ac=24,
(a2+ac)+(c2+ac)=a(a+c)+c(a+c)=(a+c)(a+c)=(a+c)2=12+24=36,
∴a+c=±6;
②∵當k≠0時,由a2+ac=12k,b2+bc=12k,得(a2+ac)﹣(b2+bc)=0,
即a2﹣b2+ac﹣bc=0,∴(a﹣b)(a+b+c)=0,
∵a≠b,∴a+b+c=0,∴b=﹣a﹣c.
由c2+ac=24k,d2+ad=24k,得(c2+ac)﹣(d2+ad)=0,即c2﹣d2+ac﹣ad=0,
∴(c﹣d)(c+d+a)=0,∵c≠d,∴c+d+a=0,∴d=﹣a﹣c,
∴b=d=﹣a﹣c,
又∵(a2+ac)×2=c2+ac=24k,∴2a(a+c)﹣c(c+a)=0,
即(a+c)(2a﹣c)=0,∴a+c=0或2a﹣c=0,
∴c=﹣a,或c=2a,又k≠0,則c=2a,
∴c=2a,b=d=﹣3a.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】某少年宮管、弦樂隊共46人.其中管樂隊人數少于23人,弦樂隊人數不足45人,現準備
購買演出服裝.下面是某服裝廠給出的演出服裝的價格
購買服裝的套數 | 1套至23套 | 24套至44套 | 45套及以上 |
每套服裝的價格 | 60元 | 50元 | 40元 |
如果管樂隊、弦樂隊分別單獨購買服裝,一共需付2500元.
(1)管樂隊、弦樂隊各多少人?
(2)如果管樂隊、弦樂隊聯合起來購買服裝.那么比兩隊各自購買服裝共可以節省多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
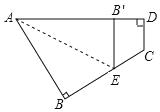
【題目】如圖所示,一個四邊形紙片 ABCD,∠B=∠D=90°,把紙片按如圖所示折疊,使點 B 落在 AD 邊上的 B′點,AE 是折痕.
(1)試判斷 B′E 與 DC 的位置關系,并說明理由;
(2)如果∠C=128°,求∠AEB 的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在銳角三角形ABC中,AB=4,△ABC的面積為8,BD平分∠ABC。若M、N分別是BD、BC上的動點,則CM+MN的最小值是( )
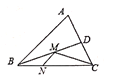
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,D是BC上的一點,且滿足∠BAD= ![]() ∠C,以AD為直徑的⊙O與AB,AC分別相交于點E,F.
∠C,以AD為直徑的⊙O與AB,AC分別相交于點E,F.
(1)求證:直線BC是⊙O的切線;
(2)連接EF,若tan∠AEF= ![]() ,AD=4,求BD的長.
,AD=4,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的直線互相垂直,垂足為D,且AC平分∠DAB.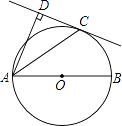
(1)求證:DC為⊙O的切線;
(2)若⊙O的半徑為5,BC=6,求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com