
 的值(用含α的式子表示出來)
的值(用含α的式子表示出來) ;(3)
;(3) .
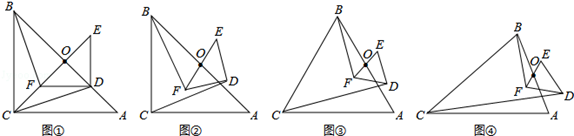
. ;(3)如答圖④所示,連接OC、OD,證明△BOF∽△COD,進而可求相似比為
;(3)如答圖④所示,連接OC、OD,證明△BOF∽△COD,進而可求相似比為 .
.


 ,∠BOC=90°
,∠BOC=90° ,∠DOF=90°.
,∠DOF=90°.
 ,∠BOF=∠COD,
,∠BOF=∠COD, .
.
 ,∠BOC=90°
,∠BOC=90° ,∠DOF=90°.
,∠DOF=90°.
 ,∠BOF=∠COD,
,∠BOF=∠COD, .
.

科目:初中數學 來源:不詳 題型:解答題
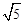 為半徑作圓,與x軸交于A、B兩點,與y軸交于C、D兩點,二次函數
為半徑作圓,與x軸交于A、B兩點,與y軸交于C、D兩點,二次函數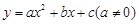 的圖象經過點A、B、C,頂點為E.
的圖象經過點A、B、C,頂點為E.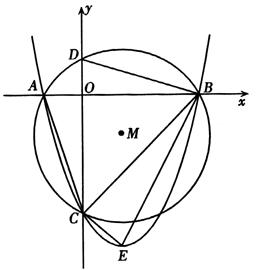
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

 cm/s速度沿AC向點C運動,同時點M從點C出發,以1cm/s的速度沿CD向點D運動,運動時間為t(t>0),連結DE并延長交正方形的邊于點F,過點M作MN⊥DF于H,交AD于N.判斷命題“當點F是邊AB中點時,則點M是邊CD的三等分點”的真假,并說明理由. (4分)
cm/s速度沿AC向點C運動,同時點M從點C出發,以1cm/s的速度沿CD向點D運動,運動時間為t(t>0),連結DE并延長交正方形的邊于點F,過點M作MN⊥DF于H,交AD于N.判斷命題“當點F是邊AB中點時,則點M是邊CD的三等分點”的真假,并說明理由. (4分)查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

| A.2:3 | B.4:9 | C.2:5 | D.4:25 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

| A.3∶5 | B.5∶3 | C.2∶5 | D.5∶2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com