
【題目】已知:函數(shù)y=ax2+x+1的圖象與x軸只有一個(gè)公共點(diǎn).
(1)求這個(gè)函數(shù)關(guān)系式;
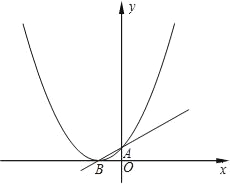
(2)如圖所示,設(shè)二次函數(shù)y=ax2+x+1圖象的頂點(diǎn)為B,與y軸的交點(diǎn)為A,P為圖象上的一點(diǎn),若以線(xiàn)段PB為直徑的圓與直線(xiàn)AB相切于點(diǎn)B,求P點(diǎn)的坐標(biāo);
(3)在(2)中,若圓與x軸另一交點(diǎn)關(guān)于直線(xiàn)PB的對(duì)稱(chēng)點(diǎn)為M,試探索點(diǎn)M是否在拋物線(xiàn)y=ax2+x+1上?若在拋物線(xiàn)上,求出M點(diǎn)的坐標(biāo);若不在,請(qǐng)說(shuō)明理由.
【答案】(1)y=x+1或y=![]() x2+x+1;(2)P點(diǎn)的坐標(biāo)為:(﹣10,16);(3)點(diǎn)M不在拋物線(xiàn)y=ax2+x+1上
x2+x+1;(2)P點(diǎn)的坐標(biāo)為:(﹣10,16);(3)點(diǎn)M不在拋物線(xiàn)y=ax2+x+1上
【解析】分析:(1)此題應(yīng)分兩種情況:①a=0,此函數(shù)是一次函數(shù),與x軸只有一個(gè)交點(diǎn);
②a≠0,此函數(shù)是二次函數(shù),可由根的判別式求出a的值,以此確定其解析式;
(2)設(shè)圓與x軸的另一個(gè)交點(diǎn)為C,連接PC,由圓周角定理知PC⊥BC;由于PB是圓的直徑,且AB切圓于B,得PB⊥AB,由此可證得△PBC∽△BAO,根據(jù)兩個(gè)相似三角形的對(duì)應(yīng)直角邊成比例,即可得到PC、BC的比例關(guān)系,可根據(jù)這個(gè)比例關(guān)系來(lái)設(shè)P點(diǎn)的坐標(biāo),聯(lián)立拋物線(xiàn)的解析式即可求出P點(diǎn)的坐標(biāo);
(3)連接CM,設(shè)CM與PB的交點(diǎn)為Q,由于C、M關(guān)于直線(xiàn)PB對(duì)稱(chēng),那么PB垂直平分CM,即CQ=QM;過(guò)M作MD⊥x軸于D,取CD的中點(diǎn)E,連接QE,則QE是Rt△CMD的中位線(xiàn);在Rt△PCB中,CQ⊥OB,QE⊥BC,易證得∠BQE、∠QCE都和∠CPQ相等,因此它們的正切值都等于![]() (在(2)題已經(jīng)求得);由此可得到CE=2QE=4BE,(2)中已經(jīng)求出了CB的長(zhǎng),根據(jù)CE、BE的比例關(guān)系,即可求出BE、CE、QE的長(zhǎng),由此可得到Q點(diǎn)坐標(biāo),也就得到M點(diǎn)的坐標(biāo),然后將點(diǎn)M代入拋物線(xiàn)的解析式中進(jìn)行判斷即可.
(在(2)題已經(jīng)求得);由此可得到CE=2QE=4BE,(2)中已經(jīng)求出了CB的長(zhǎng),根據(jù)CE、BE的比例關(guān)系,即可求出BE、CE、QE的長(zhǎng),由此可得到Q點(diǎn)坐標(biāo),也就得到M點(diǎn)的坐標(biāo),然后將點(diǎn)M代入拋物線(xiàn)的解析式中進(jìn)行判斷即可.
詳解:(1)當(dāng)a=0時(shí),y=x+1,圖象與x軸只有一個(gè)公共點(diǎn)
當(dāng)a≠0時(shí),△=1﹣4a=0,a=![]() ,此時(shí),圖象與x軸只有一個(gè)公共點(diǎn).
,此時(shí),圖象與x軸只有一個(gè)公共點(diǎn).
∴函數(shù)的解析式為:y=x+1或y=![]() x2+x+1;
x2+x+1;
(2)設(shè)P為二次函數(shù)圖象上的一點(diǎn),過(guò)點(diǎn)P作PC⊥x軸于點(diǎn)C;
∵y=ax2+x+1是二次函數(shù),由(1)知該函數(shù)關(guān)系式為:
y=![]() x2+x+1,
x2+x+1,
∴頂點(diǎn)為B(﹣2,0),圖象與y軸的交點(diǎn)
坐標(biāo)為A(0,1)
∵以PB為直徑的圓與直線(xiàn)AB相切于點(diǎn)B
∴PB⊥AB則∠PBC=∠BAO
∴Rt△PCB∽Rt△BOA
∴![]() ,故PC=2BC,
,故PC=2BC,
設(shè)P點(diǎn)的坐標(biāo)為(x,y),
∵∠ABO是銳角,∠PBA是直角,
∴∠PBO是鈍角,
∴x<﹣2
∴BC=﹣2﹣x,PC=﹣4﹣2x,
即y=﹣4﹣2x,P點(diǎn)的坐標(biāo)為(x,﹣4﹣2x)
∵點(diǎn)P在二次函數(shù)y=![]() x2+x+1的圖象上,
x2+x+1的圖象上,
∴﹣4﹣2x=![]() x2+x+1
x2+x+1
解之得:x1=﹣2,x2=﹣10
∵x<﹣2,
∴x=﹣10,
∴P點(diǎn)的坐標(biāo)為:(﹣10,16)
(3)點(diǎn)M不在拋物線(xiàn)y=ax2+x+1上
由(2)知:C為圓與x軸的另一交點(diǎn),連接CM,CM與直線(xiàn)PB的交點(diǎn)為Q,過(guò)點(diǎn)M作x軸的垂線(xiàn),垂足為D,取CD的中點(diǎn)E,連接QE,則CM⊥PB,且CQ=MQ,即QE是中位線(xiàn).
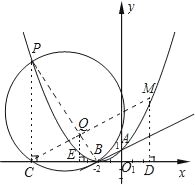
∴QE∥MD,QE=![]() MD,QE⊥CE
MD,QE⊥CE
∵CM⊥PB,QE⊥CE,PC⊥x軸
∴∠QCE=∠EQB=∠CPB
∴tan∠QCE=tan∠EQB=tan∠CPB=![]()
CE=2QE=2×2BE=4BE,又CB=8,
故BE=![]() ,QE=
,QE=![]()
∴Q點(diǎn)的坐標(biāo)為(﹣![]() ,
,![]() )
)
可求得M點(diǎn)的坐標(biāo)為(![]() ,
,![]() )
)
∵![]()
∴C點(diǎn)關(guān)于直線(xiàn)PB的對(duì)稱(chēng)點(diǎn)M不在拋物線(xiàn)y=ax2+x+1上.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】中考體育測(cè)試前,某區(qū)教育局為了了解選報(bào)引體向上的初三男生的成績(jī)情況,隨機(jī)抽測(cè)了本區(qū)部分選報(bào)引體向上項(xiàng)目的初三男生的成績(jī),并將測(cè)試得到的成績(jī)繪成了下面兩幅不完整的統(tǒng)計(jì)圖:
請(qǐng)你根據(jù)圖中的信息,解答下列問(wèn)題:
(![]() )寫(xiě)出扇形圖中
)寫(xiě)出扇形圖中![]() __________
__________![]() ,并補(bǔ)全條形圖.
,并補(bǔ)全條形圖.
(![]() )在這次抽測(cè)中,測(cè)試成績(jī)的眾數(shù)和中位數(shù)分別是__________個(gè)、__________個(gè).
)在這次抽測(cè)中,測(cè)試成績(jī)的眾數(shù)和中位數(shù)分別是__________個(gè)、__________個(gè).
(![]() )該區(qū)體育中考選報(bào)引體向上的男生共有
)該區(qū)體育中考選報(bào)引體向上的男生共有![]() 人,如果體育中考引體向上達(dá)
人,如果體育中考引體向上達(dá)![]() 個(gè)以上(含
個(gè)以上(含![]() 個(gè))得滿(mǎn)分,請(qǐng)你估計(jì)該區(qū)體育中考中選報(bào)引體向上的男生能獲得滿(mǎn)分的有多少名?
個(gè))得滿(mǎn)分,請(qǐng)你估計(jì)該區(qū)體育中考中選報(bào)引體向上的男生能獲得滿(mǎn)分的有多少名?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2014年1月,國(guó)家發(fā)改委出臺(tái)指導(dǎo)意見(jiàn),要求2015年底前,所有城市原則上全面實(shí)行居民階梯水價(jià)制度.小明為了解市政府調(diào)整水價(jià)方案的社會(huì)反響,隨機(jī)訪(fǎng)問(wèn)了自己居住在小區(qū)的部分居民,就“每月每戶(hù)的用水量”和“調(diào)價(jià)對(duì)用水行為改變”兩個(gè)問(wèn)題進(jìn)行調(diào)查,并把調(diào)查結(jié)果整理成下面的圖1,圖2.

小明發(fā)現(xiàn)每月每戶(hù)的用水量在5m2-35m2之間,有8戶(hù)居民對(duì)用水價(jià)格調(diào)價(jià)漲幅抱無(wú)所謂,不用考慮用水方式的改變.根據(jù)小明繪制的圖表和發(fā)現(xiàn)的信息,完成下列問(wèn)題:
(1)n= ,小明調(diào)查了 戶(hù)居民,并補(bǔ)全圖1;
(2)每月每戶(hù)用水量的中位數(shù)和眾數(shù)分別落在什么范圍?
(3)如果小明所在的小區(qū)有1800戶(hù)居民,請(qǐng)你估計(jì)“視調(diào)價(jià)漲幅采取相應(yīng)的用水方式改變”的居民戶(hù)數(shù)有多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
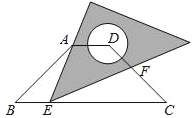
【題目】如圖,在等腰梯形ABCD中,AD∥BC,BC=4AD=4![]() ,∠B=45°.直角三角板含45°角的頂點(diǎn)E在邊BC上移動(dòng),一直角邊始終經(jīng)過(guò)點(diǎn)A,斜邊與CD交于點(diǎn)F.若△ABE為等腰三角形,則CF的長(zhǎng)等于_____.
,∠B=45°.直角三角板含45°角的頂點(diǎn)E在邊BC上移動(dòng),一直角邊始終經(jīng)過(guò)點(diǎn)A,斜邊與CD交于點(diǎn)F.若△ABE為等腰三角形,則CF的長(zhǎng)等于_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直角坐標(biāo)系中,點(diǎn)A、B的坐標(biāo)分別為(1,4)和(3,0),點(diǎn)C是y軸上的一個(gè)動(dòng)點(diǎn),且A、B、C三點(diǎn)不在同一條直線(xiàn)上,當(dāng)△ABC的周長(zhǎng)最小時(shí),點(diǎn)C的坐標(biāo)是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,點(diǎn)A的坐標(biāo)是(1,3),將點(diǎn)A繞原點(diǎn)O順時(shí)針旋轉(zhuǎn)90°得到點(diǎn)A′,則點(diǎn)A′的坐標(biāo)是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出以下命題:
①函數(shù)![]() 是偶函數(shù),但不是奇函數(shù);
是偶函數(shù),但不是奇函數(shù);
②已知回歸直線(xiàn)方程為![]() ,樣本點(diǎn)的中心為
,樣本點(diǎn)的中心為![]() ,則
,則![]() ;
;
③函數(shù)![]() 圖象關(guān)于點(diǎn)
圖象關(guān)于點(diǎn)![]() 對(duì)稱(chēng)且在
對(duì)稱(chēng)且在![]() 上單調(diào)遞增;
上單調(diào)遞增;
④根據(jù)黨中央關(guān)于“精準(zhǔn)”脫貧的要求,我州某農(nóng)業(yè)經(jīng)濟(jì)部門(mén)決定派出五位相關(guān)專(zhuān)家對(duì)三個(gè)貧困地區(qū)進(jìn)行調(diào)研,每個(gè)地區(qū)至少派遣一位專(zhuān)家,其中甲、乙兩位專(zhuān)家需要派遣至同一地區(qū),則不同的派遣方案種數(shù)有![]() 種;
種;
⑤已知雙曲線(xiàn)![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,過(guò)
,過(guò)![]() 的直線(xiàn)交雙曲線(xiàn)右支于
的直線(xiàn)交雙曲線(xiàn)右支于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,若
,若![]() ,則雙曲線(xiàn)的離心率為
,則雙曲線(xiàn)的離心率為![]() .
.
其中正確的命題序號(hào)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有20筐白菜,以每筐25千克為標(biāo)準(zhǔn),超過(guò)或不足的千克數(shù)分別用正、負(fù)數(shù)來(lái)表示,記錄如下:
與標(biāo)準(zhǔn)質(zhì)量的差值(單位:千克) |
|
|
| 0 | 1 | 2.5 |
筐數(shù) | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最輕的一筐多重多少千克?
(2)與標(biāo)準(zhǔn)重量比較,20筐白菜總計(jì)超過(guò)或不足多少千克?
(3)若白菜每千克售價(jià)2.8元,則出售這20筐白菜可賣(mài)多少元?(結(jié)果保留整數(shù))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
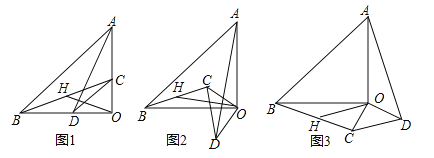
【題目】(2017黑龍江省龍東地區(qū))已知:△AOB和△COD均為等腰直角三角形,∠AOB=∠COD=90°.連接AD,BC,點(diǎn)H為BC中點(diǎn),連接OH.
(1)如圖1所示,易證:OH=![]() AD且OH⊥AD(不需證明)
AD且OH⊥AD(不需證明)
(2)將△COD繞點(diǎn)O旋轉(zhuǎn)到圖2,圖3所示位置時(shí),線(xiàn)段OH與AD又有怎樣的關(guān)系,并選擇一個(gè)圖形證明你的結(jié)論.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com