
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4)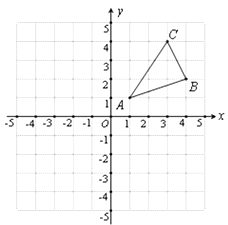
⑴ 作出與△ABC關于y軸對稱△A1B1C1 , 并寫出三個頂點的坐標為:A1(),B1(),C1();
【答案】-1,1;-4,2;-3,4
⑵ 在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標;
解:如圖1,找出A的對稱點A′(1,﹣1),連接BA′,與x軸交點即為P,點P坐標為(2,0);
⑶ 在 y 軸上是否存在點 Q,使得S△AOQ= ![]() S△ABC , 如果存在,求出點 Q 的坐標,如果不存在,說明理由。
S△ABC , 如果存在,求出點 Q 的坐標,如果不存在,說明理由。
解:設存在點 Q,使得S△AOQ= ![]() S△ABC , 如圖2,作AD⊥y軸于D,設Q點坐標為(0,y),則 OQ=|y|,AD=1,
S△ABC , 如圖2,作AD⊥y軸于D,設Q點坐標為(0,y),則 OQ=|y|,AD=1,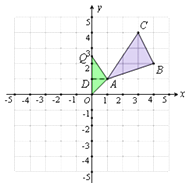
S△ABC= ![]() =
= ![]() ,
,
由題意,S△AOQ= ![]() S△ABC , 得
S△ABC , 得 ![]() ,
,![]() 或
或 ![]() ,
,
∴ Q點坐標為(0, ![]() )或(0,
)或(0, ![]() )
)
【解析】解:(1)△A1B1C1如圖所示,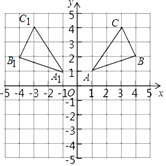
A1(-1,1),B1(-4,2),C1(-3,4);
故答案為:-1,1;-4,2;-3,4;
(1)根據關于y軸對稱點的坐標特點可求出;
(2)找出A的對稱點A′,連接BA′,與x軸交點即為P,從而得到P點的坐標;
(3)設存在點 Q,作AD⊥y軸于D,設Q點坐標為(0,y),則 OQ=|y|,AD=1.先求出△ABC的面積,從而可得△AOQ的面積,再由△AOQ的面積公式可求出y的值,即可得Q的坐標.


 小學教材全測系列答案
小學教材全測系列答案科目:初中數學 來源: 題型:
【題目】初三(1)班要從甲、乙、丙、丁這![]() 名同學中隨機選取
名同學中隨機選取![]() 名同學參加學校畢業生代表座談會.求下列事件的概率:
名同學參加學校畢業生代表座談會.求下列事件的概率:
(![]() )已確定甲參加,另外
)已確定甲參加,另外![]() 人恰好選中乙;
人恰好選中乙;
(![]() )隨機選取
)隨機選取![]() 名同學,恰好選中甲和乙.
名同學,恰好選中甲和乙.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小敏進行賽跑訓練,他們選擇了一個土坡,按同一路線同時出發,從坡腳跑到坡頂再原路返回坡腳.他們倆上坡的平均速度不同,下坡的平均速度則是各自上坡平均速度的![]() 倍.設兩人出發
倍.設兩人出發![]() 后距出發點的距離為ym.圖中折線段
后距出發點的距離為ym.圖中折線段![]() 表示小明在整個訓練中y與x的函數關系.
表示小明在整個訓練中y與x的函數關系.
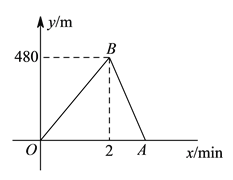
(![]() )點
)點![]() 所表示的實際意義是__________.
所表示的實際意義是__________.
(![]() )求
)求![]() 所在直線的函數表達式.
所在直線的函數表達式.
(![]() )如果小敏上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?
)如果小敏上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在湖邊高出水面50m的山頂A處看見一艘飛艇停留在湖面上空某處,觀察到飛艇底部標志P處的仰角為45°,又觀其在湖中之像的俯角為60°,則飛艇底部P距離湖面的高度為(參考等式: ![]() )( )
)( )
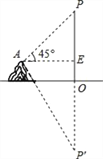
A. 25![]() +75 B. 50
+75 B. 50![]() +50 C. 75
+50 C. 75![]() +75 D. 50
+75 D. 50![]() +100
+100
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com