
【題目】如圖,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分別與⊙O相切于E,F(xiàn),G三點,過點D作⊙O的切線BC于點M,切點為N,則DM的長為( )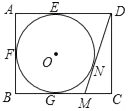
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】連接OE,OF,ON,OG,
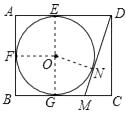
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分別與⊙O相切于E,F(xiàn),G三點,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四邊形AFOE,F(xiàn)BGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切線,
∴DN=DE=3,MN=MG,
∴CM=5﹣2﹣MN=3﹣MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3﹣NM)2+42,
∴NM= ![]() ,
,
∴DM=3 ![]() =
= ![]() ,
,
故答案為:A.
易得四邊形ABMD外切于⊙O,由切線的性質(zhì)易得∠AEO=∠AFO=∠OFB=∠BGO=90°,四邊形AFOE,F(xiàn)BGO是正方形;AF=BF=AE=BG=2,DE=3。在R t△CDM中,利用MN表示三邊,再利用勾股定理可得MN的值,最后可得DM的值。


 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:初中數(shù)學(xué) 來源: 題型:
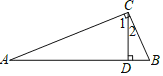
【題目】如圖,直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .
.
(1)找出圖中相等的銳角,并說明理由.
(2)求出點![]() 到直線
到直線![]() 的距離以及點
的距離以及點![]() 到直線
到直線![]() 的距離.
的距離.
解:(1)![]() (已知),
(已知),
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
同理可證,
![]() .
.
(2)點![]() 到直線
到直線![]() 的距離
的距離![]()
![]() .
.
![]() 到直線
到直線![]() 的距離為線段 的長度.
的距離為線段 的長度.
![]()
![]()
![]()
![]() (填線段名稱).
(填線段名稱).
![]() ,
,![]() ,
,![]() ,代入上式,解得
,代入上式,解得
![]()
![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合與實踐:在綜合實踐課上,老師讓同學(xué)們在已知三角形的基礎(chǔ)上,經(jīng)過畫圖,探究三角形邊之間存在的關(guān)系.如圖,已知點![]() 在
在![]() 的邊
的邊![]() 的延長線上,過點
的延長線上,過點![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交線段
交線段![]() 于點
于點![]() .
.

實踐操作
(1)尺規(guī)作圖:作出符合上述條件的圖形;
探究發(fā)現(xiàn)
(2)勤奮小組在作出圖形后,發(fā)現(xiàn)![]() ,
,![]() ,請說明理由;
,請說明理由;
探究應(yīng)用
(3)縝密小組在勤奮小組探究的基礎(chǔ)上,測得![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
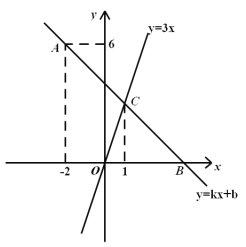
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖像經(jīng)過點
的圖像經(jīng)過點![]() ,且與
,且與![]() 軸相交于點
軸相交于點![]() ,與正比例函數(shù)
,與正比例函數(shù)![]() 的圖像交于點
的圖像交于點![]() ,點
,點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
(1)求![]()
![]() 的值;
的值;
(2)若點![]() 在
在![]() 軸上,且滿足
軸上,且滿足![]() ,求點
,求點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解全區(qū)5000名初中畢業(yè)生的體重情況,隨機抽測了400名學(xué)生的體重,頻率分布如圖所示(每小組數(shù)據(jù)可含最小值,不含最大值),其中從左至右前四個小長方形的高依次為0.02、0.03、0.04、0.05,由此可估計全區(qū)初中畢業(yè)生的體重不小于60千克的學(xué)生人數(shù)約為人. 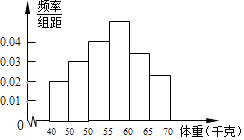
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com