
【題目】如圖,從一張腰長為60cm,頂角為120°的等腰三角形鐵皮OAB中剪出一個最大的扇形OCD,用此剪下的扇形鐵皮圍成一個圓錐的側面(不計損耗),則該圓錐的高為( ) 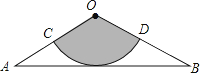
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
科目:初中數學 來源: 題型:
【題目】如圖,某飛機于空中探測某座山的高度,在點A處飛機的飛行高度是AF=3700米,從飛機上觀測山頂目標C的俯角是45°,飛機繼續以相同的高度飛行300米到B處,此時觀測目標C的俯角是50°,求這座山的高度CD.
(參考數據:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+9的頂點為A,曲線DE是雙曲線y= ![]() (3≤x≤12)的一部分,記作G1 , 且D(3,m)、E(12,m﹣3),將拋物線y=﹣x2+9水平向右移動a個單位,得到拋物線G2 .
(3≤x≤12)的一部分,記作G1 , 且D(3,m)、E(12,m﹣3),將拋物線y=﹣x2+9水平向右移動a個單位,得到拋物線G2 . 
(1)求雙曲線的解析式;
(2)設拋物線y=﹣x2+9與x軸的交點為B、C,且B在C的左側,則線段BD的長為;
(3)點(6,n)為G1與G2的交點坐標,求a的值.
(4)解:在移動過程中,若G1與G2有兩個交點,設G2的對稱軸分別交線段DE和G1于M、N兩點,若MN< ![]() ,直接寫出a的取值范圍.
,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系內,小正方形網格的邊長為1個單位長度,△ABC的三個頂點的坐標分別為A(﹣1,3),B(﹣4,0),C(0,0)
(1)畫出將△ABC向上平移1個單位長度,再向右平移5個單位長度后得到的△A1B1C1;
(2)畫出將△ABC繞原點O順時針方向旋轉90°得到△A2B2O;
(3)在x軸上存在一點P,滿足點P到A1與點A2距離之和最小,請直接寫出P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,BD為⊙O的直徑,BD與AC相交于點H,AC的延長線與過點B的直線相交于點E,且∠A=∠EBC.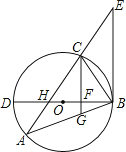
(1)求證:BE是⊙O的切線;
(2)已知CG∥EB,且CG與BD、BA分別相交于點F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,⊙M與x軸相切于原點,平行于y軸的直線交圓于P,Q兩點,P點在Q點的下方,若P點坐標是(2,1),則圓心M的坐標是( )
A.(0,3)
B.(0,2)
C.(0,![]() )
)
D.(0,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB,AD與⊙O相切于點B,D,C為⊙O上一點,且∠BCD=140°,則∠A的度數是( ) 
A.70°
B.105°
C.100°
D.110°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D是BC上一點,∠DAC=∠B,E為AB上一點. 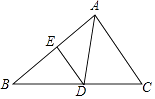
(1)求證:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的長;
(3)在(2)的條件下,若DE∥AC,AE=4,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com