
【題目】如圖,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一邊QP在BC邊上,E、F分別在AB、AC上,AD交EF于點H.
(1)當矩形EFPQ為正方形時,求正方形的邊長;
(2)設EF=x,當x為何值時,矩形EFPQ的面積最大?并求出最大面積;
(3)當矩形EFPQ的面積最大時,該矩形EFPQ以每秒1個單位的速度沿射線BC勻速向右運動(當矩形的頂點Q到達C點時停止運動),設運動時間為t秒,矩形EFPQ與△ABC重疊部分的面積為S,求S與t的函數關系式,并寫出t的取值范圍.

【答案】(1)當矩形EFPQ為正方形時,邊長為![]() ;(2)當x=
;(2)當x=![]() 時,矩形EFPQ的面積最大,最大面積為5;(3)當0≤t≤
時,矩形EFPQ的面積最大,最大面積為5;(3)當0≤t≤![]() 時,S =5-2t2;當
時,S =5-2t2;當![]() <t<2.5時,S=
<t<2.5時,S=![]() -2t;當2.5≤t≤3時,S=2t2-12t+18
-2t;當2.5≤t≤3時,S=2t2-12t+18
【解析】(1)由條件可得![]() ,即
,即![]() ,計算即可.
,計算即可.
(2)可利用![]() 用x表示出EH.表示出矩形EFPQ的面積,利用二次函數可求得其最大值;
用x表示出EH.表示出矩形EFPQ的面積,利用二次函數可求得其最大值;
(3)分0≤t≤![]() ,
,![]() ,2.5≤t≤3三種情況進行討論即可.
,2.5≤t≤3三種情況進行討論即可.
(1)∵四邊形EFPQ為矩形,
∴EF∥BC,
![]() ,
,
即![]() ,
,
解得![]()
∴當矩形EFPQ為正方形時,邊長為![]() .
.
即當x為![]() 時,矩形EFPQ為正方形;
時,矩形EFPQ為正方形;
(2)∵∠B=45°,
∴![]() ,
,
∴![]()
∵EF∥BC,
∴△AEH∽△ABD,∴![]() ,
,
∵EF∥BC,∴△AFH∽△ACD,∴![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
已知EF=x,則EH=![]() .
.
∵∠B=45°,
∴![]() =4﹣
=4﹣![]() .
.
S矩形EFPQ![]()
∴當x=![]() 時,矩形EFPQ的面積最大,最大面積為5.
時,矩形EFPQ的面積最大,最大面積為5.
(3)如圖①,當0≤t≤![]() 時
時

設EF交AC于M點,FP交AC于N點,
∵△MNF∽△CAD,
∴![]() ,
,
即![]() ,
,
∴FN=4t ,
∴S=5-![]() t·4t,
t·4t,
=5-2t2
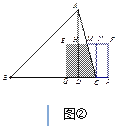
如圖②,當![]() 時
時
設EF交AC于M點,過C作CN⊥EF于N點,
∵△CNM∽△ADC
∴![]() ,
,
即![]() ,
,
∴MN=![]() ,
,
∴FN=t-![]() ,
,
∴S=5-![]() (t-
(t-![]() +t),
+t),
=![]() -2t ,
-2t ,
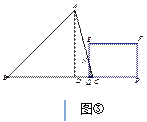
如圖③,當2.5≤t≤3時
設EQ交AC于N點,
∵△CQN∽△CDA
∴![]() ,
,
![]() ,
,
∴NQ=12-4t,
∴S=![]() (3-t)(12-4t)
(3-t)(12-4t)
=2t2-12t+18


科目:初中數學 來源: 題型:
【題目】如圖,數軸的原點為0,點A、B、C是數軸上的三點,點B對應的數位1,AB=6,BC=2,動點P、Q同時從A、C出發,分別以每秒2個長度單位和每秒1個長度單位的速度沿數軸正方向運動.設運動時間為t秒(t>0)
(1)求點A、C分別對應的數;
(2)經過t秒后,求點P、Q分別對應的數(用含t的式子表示)
(3)試問當t為何值時,OP=OQ?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
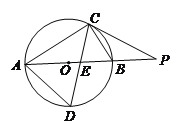
【題目】如圖,⊙O的直徑AB為2cm,弦BC為1cm,∠ACB的平分線與⊙O交于點D,與AB交于點E,P為AB延長線上一點,連接PC,且PC=PE.
(1)求AC、AD的長;
(2)試判斷直線PC與⊙O的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 是
是![]() 邊上的一點,
邊上的一點,![]() 是
是![]() 的中點,過點
的中點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 的延長線于
的延長線于![]() ,且
,且![]() ,連結
,連結![]() .
.
(1)求證:![]() 是
是![]() 的中點;
的中點;
(2)如果![]() ,試猜測四邊形
,試猜測四邊形![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,將△ABD沿AB所在的直線折疊,使點D落在點E處;將△ACD沿AC所在的直線折疊,使點D落在點F處,分別延長EB、FC使其交于點M.
(1)判斷四邊形AEMF的形狀,并給予證明.
(2)設AD=x,利用勾股定理,建立關于x的方程模型,求四邊形AEMF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知線段![]() 和線段
和線段![]() .
.

(1)按要求作圖(保留作圍痕跡,不寫作法);
延長線段![]() 至點
至點![]() ,使
,使![]() ,反向延長線段
,反向延長線段![]() 至點
至點![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點,且
的中點,且![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 經過
經過![]() 頂點
頂點![]() 的一條直線,
的一條直線,![]() .
.![]() 分別是直線
分別是直線![]() 上兩點,且
上兩點,且![]() .
.
(1)若直線![]() 經過
經過![]() 的內部,且
的內部,且![]() 在射線
在射線![]() 上,請解決下面兩個問題:
上,請解決下面兩個問題:
①如圖1,若![]() ,
,![]() ,
,
則![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如圖2,若![]() ,請添加一個關于
,請添加一個關于![]() 與
與![]() 關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
(2)如圖3,若直線![]() 經過
經過![]() 的外部,
的外部,![]() ,請提出
,請提出![]() 三條線段數量關系的合理猜想(不要求證明).
三條線段數量關系的合理猜想(不要求證明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com