
【題目】若關于x的一元二次方程 ![]() x2+
x2+ ![]() x+tana=0有兩個相等的實數根,則銳角a等于( )
x+tana=0有兩個相等的實數根,則銳角a等于( )
A.15°
B.30°
C.45°
D.60°
科目:初中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)證明:k∈R,直線y=g(x)都不是曲線y=f(x)的切線;
(2)若x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立,求實數k的取值范圍.
成立,求實數k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從﹣3,﹣1, ![]() ,1,3這五個數中,隨機抽取一個數,記為a,若數a使關于x的不等式組
,1,3這五個數中,隨機抽取一個數,記為a,若數a使關于x的不等式組  無解,且使關于x的分式方程
無解,且使關于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整數解,那么這5個數中所有滿足條件的a的值之和是( )
=﹣1有整數解,那么這5個數中所有滿足條件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在關于x的分式方程 ![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均為實數,方程①的根為非負數.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均為實數,方程①的根為非負數.
(1)求k的取值范圍;
(2)當方程②有兩個整數根x1、x2 , k為整數,且k=m+2,n=1時,求方程②的整數根;
(3)當方程②有兩個實數根x1、x2 , 滿足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k為負整數時,試判斷|m|≤2是否成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某運動員在一場籃球比賽中的技術統計如表所示:
技術 | 上場時間(分鐘) | 出手投籃(次) | 投中 | 罰球得分 | 籃板 | 助攻(次) | 個人總得分 |
數據 | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
注:表中出手投籃次數和投中次數均不包括罰球.
根據以上信息,求本場比賽中該運動員投中2分球和3分球各幾個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,線段AB經過平移得到線段A′B′,其中點A,B的對應點分別為點A′,B′,這四個點都在格點上,則這四個點組成的四邊形ABB′A′的面積是( )
A.4
B.6
C.9
D.13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條筆直的公路的同側依次排列著A,C,B三個村莊,某天甲、乙兩車分別從A,B兩地出發,沿這條公路勻速行駛至C地停止,從甲車出發至甲車到達C地的過程,甲、乙兩車各自與C地的距離y(km)與甲車行駛時間t(h)之間的函數關系如圖所示.求: 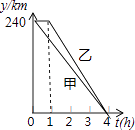
(1)甲的速度是 , 乙的速度是;
(2)分別求出甲、乙兩車各自與C地的距離y(km)與甲車行駛時間t(h)之間的函數關系式,并寫出取值范圍;
(3)若甲、乙兩車到C地后繼續沿該公路原速度行駛,求甲車出發多少小時,兩車相距350km.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:
①四邊形CFHE是菱形;
②EC平分∠DCH;
③線段BF的取值范圍為3≤BF≤4;
④當點H與點A重合時,EF=2 ![]() .
.
以上結論中,你認為正確的有 . (填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在Rt△ACB中,C為直角頂點,∠ABC=25°,O為斜邊中點.將OA繞著點O逆時針旋轉θ°(0<θ<180)至OP,當△BCP恰為軸對稱圖形時,θ的值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com