
【題目】如圖1,在平面直角坐標系中,直線![]() 經過點
經過點![]() ,與
,與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,點
兩點,點![]() ,
,![]()
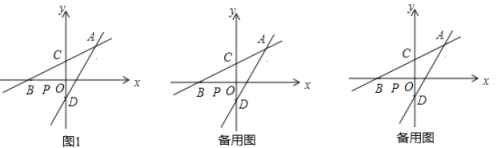
(1)求![]() 的值和直線
的值和直線![]() 的函數表達式;
的函數表達式;
(2)連結![]() ,當
,當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的值;
的值;
(3)若![]() ,點
,點![]() ,
,![]() 分別在線段
分別在線段![]() ,線段
,線段![]() 上,當
上,當![]() 是等腰直角三角形且
是等腰直角三角形且![]() 時,則
時,則![]() 的面積是______.
的面積是______.
【答案】(1)![]() ,直線AD的表達式為:
,直線AD的表達式為:![]() (2)t的值為
(2)t的值為![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 的面積是
的面積是![]() 或
或![]() .
.
【解析】
(1)將A點代入![]() 即可求得m的值, 根據D點設直線AD的一般式,將A點代入求得k的值即可;
即可求得m的值, 根據D點設直線AD的一般式,將A點代入求得k的值即可;
(2)分以BC為底和以BC為腰(其中BC為腰又分為以B點為頂點和以C點為頂點分別討論)兩種情況討論,畫出相應的圖形,根據圖形分析即可得出t的值;
(3)分以M為直角頂點和以N為直角頂點,構造全等三角形,進行分析即可求出![]() 的面積.
的面積.
解:(1)將![]() 代入
代入![]() 中的得
中的得![]() ,解得
,解得![]() ,
,
因為![]() ,所以設直線AD的解析式為:
,所以設直線AD的解析式為:![]() ,
,
將![]() 代入得
代入得![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
(2)如下圖,
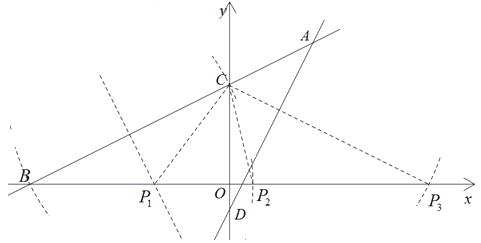
由直線![]() 可知
可知![]() ,
,
當y=0時,![]() ,解得x=-8,所以
,解得x=-8,所以![]() ,
,
①當等腰![]() 以BC為底時,P點在BC的垂直平分線與x軸交點
以BC為底時,P點在BC的垂直平分線與x軸交點![]() 處,
處,
則此時![]() ,
,
即![]() ,解得
,解得![]() ;
;
②當等腰![]() 以BC為腰時,若B點為頂點,則以B點為圓心,BC為半徑畫弧,在B點右側(因為
以BC為腰時,若B點為頂點,則以B點為圓心,BC為半徑畫弧,在B點右側(因為![]() )與x軸相交于
)與x軸相交于![]() ,
,
∵![]() ,
,
∴![]() ,
,
若C點為頂點,則以C點為圓心,BC為半徑畫弧,與x正半軸交于![]() 處,
處,
![]()
∴![]() ,即
,即![]() ,
,
綜上所述t的值為![]() 或
或![]() 或
或![]() .
.
(3)①當![]() 是以M為直角頂點的等腰直角三角形,如下圖,
是以M為直角頂點的等腰直角三角形,如下圖,
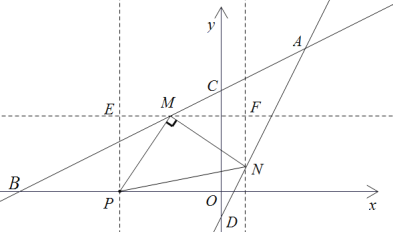
分別過P點和N點作x軸垂線與過M點作y軸的垂線相交于E,F,
則∵EP垂直x軸,FN垂直x軸,EF垂直y軸
∴∠PEF=∠EFN=90°,
∴∠EPM+∠EMP=90°,
∵∠PMN=90°,
∴∠FMN+∠EMP=90°,
∴∠EPM=∠FMN,
又∵PM=MN,
∴△PEM≌△MFN
∴設MF=EP=m,NF=ME=n,
∵P(-4,0),
∴![]() ,
,
分別將M和N代入![]() 和
和![]() 中
中
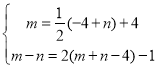 解得
解得![]() ,
,
∴![]() ,
,![]() ;
;
當![]() 是以N為直角頂點的等腰直角三角形,如下圖,
是以N為直角頂點的等腰直角三角形,如下圖,
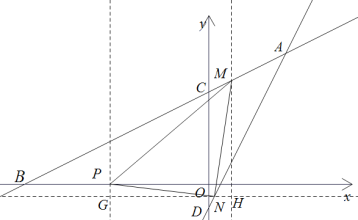
分別過P點和M點作x軸垂線與過N點作y軸的垂線相交于G,H,
與本小題①同理可證△NPG≌△MNH
設![]() ,
,
則![]()
分別將M和N代入![]() 和
和![]() 中,
中,
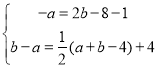 ,解得
,解得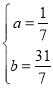
所以![]() ,
,![]()
故![]() 的面積是
的面積是![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】某工程,乙工程隊單獨先做10天后,再由甲、乙兩個工程隊合作20天就能完成全部工作,已知甲工程隊單獨完成此工程所需天數是乙工程隊單獨完成此工程所需天數的![]() .
.
(1)求甲、乙工程隊單獨完成此工程各需多少天;
(2)甲工程隊每天的費用為0.67萬元,乙工程每天的費用為0.33萬元,該工程的預算費用為20萬元,若甲、乙工程隊一起合作完成該工程,請問工程費用是否夠用?若不夠用,應追加多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
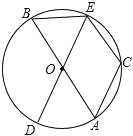
【題目】如圖,在⊙O中,AB、DE為⊙O的直徑,C是⊙O上一點,且![]() =
=![]() .
.
(1)BE與CE有什么數量關系?為什么?
(2)若∠BOE=60°,則四邊形OACE是什么特殊的四邊形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是圓O的切線,切點為A,AB是圓O的弦。過點B作BC//AD,交圓O于點C,連接AC,過點C作CD//AB,交AD于點D。連接AO并延長交BC于點M,交過點C的直線于點P,且BCP=ACD。
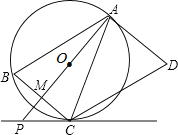
(1)判斷直線PC與圓O的位置關系,并說明理由:
(2) 若AB=9,BC=6,求PC的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠A=30°,以AB為直徑的⊙O交BC于點D,交AC于點E,連結DE,過點B作BP平行于DE,交⊙O于點P,連結EP、CP、OP.
(1)BD=DC嗎?說明理由;
(2)求∠BOP的度數;
(3)求證:CP是⊙O的切線.
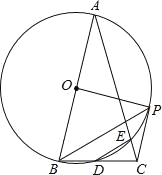
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在⊙O上,D是![]() 中點,若∠BAC=70°,求∠C.
中點,若∠BAC=70°,求∠C.
下面是小雯的解法,請幫他補充完整.
解:在⊙O中,
∵D是![]() 的中點
的中點
∴![]() =
=![]() ,
,
∴∠l=∠2( )(填推理的依據)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直徑,
∴∠ADB=90°( )(填推理的依據)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四個點都在⊙O上,
∴∠C+∠B=180°( )(填推理的依據)
∴∠C=l80°﹣∠B= (填計算結果)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自2017年3月起,成都市中心城區居民用水實行以戶為單位的三級階梯收費辦法:
第I級:居民每戶每月用水18噸以內含18噸每噸收水費a元;
第Ⅱ級:居民每戶每月用水超過18噸但不超過25噸,未超過18噸的部分按照第Ⅰ級標準收費,超過部分每噸收水費b元;
第Ⅲ級:居民每戶每月用水超過25噸,未超過25噸的部分按照第I、Ⅱ級標準收費,超過部分每噸收水費c元.
設一戶居民月用水x噸,應繳水費為y元,y與x之間的函數關系如圖所示
(1)根據圖象直接作答:a= ,b= ;
(2)求當x≥25時y與x之間的函數關系;
(3)把上述水費階梯收費辦法稱為方案①,假設還存在方案②:居民每戶月用水一律按照每噸4元的標準繳費,請你根據居民每戶月“用水量的大小設計出對居民繳費最實惠的方案.(寫出過程)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(定義)如圖1,A,B為直線l同側的兩點,過點A作直線1的對稱點A′,連接A′B交直線l于點P,連接AP,則稱點P為點A,B關于直線l的“等角點”.
(運用)如圖2,在平面直坐標系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )兩點.
)兩點.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三點中,點 是點A,B關于直線x=4的等角點;
)三點中,點 是點A,B關于直線x=4的等角點;
(2)若直線l垂直于x軸,點P(m,n)是點A,B關于直線l的等角點,其中m>2,∠APB=α,求證:tan![]() =
=![]() ;
;
(3)若點P是點A,B關于直線y=ax+b(a≠0)的等角點,且點P位于直線AB的右下方,當∠APB=60°時,求b的取值范圍(直接寫出結果).
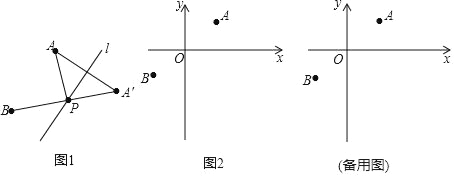
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com