
【題目】如圖22,在∠AOB的兩邊OA,OB上分別取OM=ON,OD=OE,DN和EM相交于點C.求證:點C在∠AOB的平分線上.
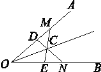
【答案】見解析
【解析】
過點C分別作CG⊥OA于點G,CF⊥OB于點F,在△MOE和△NOD中,根據OM=ON,∠MOE=∠NOD,OE=OD,可判定△MOE≌△NOD,根據全等三角形的性質可得:S△MOE=S△NOD,繼而可得S△MOE-S四邊形ODCE=S△NOD-S四邊形ODCE,即S△MDC=S△NEC.
由三角形面積公式得DM·CG=EN·CF.由于OM=ON,OD=OE,所以DM=EN,CG=CF.
根據CG⊥OA,CF⊥OB,可證點C在∠AOB的平分線上.
證明:過點C分別作CG⊥OA于點G,CF⊥OB于點F,
如圖.

在△MOE和△NOD中,OM=ON,∠MOE=∠NOD,OE=OD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四邊形ODCE=S△NOD-S四邊形ODCE,
即S△MDC=S△NEC.
由三角形面積公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN,
∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴點C在∠AOB的平分線上.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
【題目】某校七年級共有500名學生,團委準備調查他們對“低碳”知識的了解程度,
(1)在確定調查方式時,團委設計了以下三種方案:
方案一:調查七年級部分女生;
方案二:調查七年級部分男生;
方案三:到七年級每個班去隨機調查一定數量的學生
請問其中最具有代表性的一個方案是 ;
(2)團委采用了最具有代表性的調查方案,并用收集到的數據繪制出兩幅不完整的統計圖(如圖①、圖②所示),請你根據圖中信息,將其補充完整;
(3)請你估計該校七年級約有多少名學生比較了解“低碳”知識.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC邊上,且BE=BD,連結AE、DE、DC.
①求證:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度數.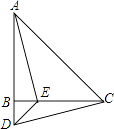
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD、![]() 分別是銳角三角形ABC和銳角三角形
分別是銳角三角形ABC和銳角三角形![]() 中BC、
中BC、![]() 邊上的高,且
邊上的高,且![]() 、
、![]() .若使△ABC≌△
.若使△ABC≌△![]() ,請你補充條件_________.(填寫一個你認為適當的條件即可)
,請你補充條件_________.(填寫一個你認為適當的條件即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小宇想測量位于池塘兩端的A、B兩點的距離.他沿著與直線AB平行的道路EF行走,當行走到點C處,測得∠ACF=45°,再向前行走100米到點D處,測得∠BDF=60°.若直線AB與EF之間的距離為60米,求A、B兩點的距離. 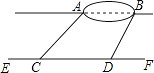
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,邊長不等的正方形依次排列,每個正方形都有一個頂點落在函數y=x的圖象上,從左向右第3個正方形中的一個頂點A的坐標為(8,4),陰影三角形部分的面積從左向右依次記為S1、S2、S3、…、Sn , 則Sn的值為 . (用含n的代數式表示,n為正整數) 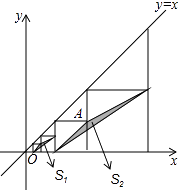
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某食品廠從生產的袋裝食品中抽出樣品 20 袋,檢測每袋的質量是否符合標準,超過或不足的部分分別用正、負數來表示,記錄如下表:

①這批樣品的平均質量比標準質量多還是少?用你學過的方法合理解釋;
②若標準質量為 450 克,則抽樣檢測的總質量是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com