
【題目】已知ai≠0(i=1,2,…,2012)滿足 ![]() ,使直線y=aix+i(i=1,2,…,2012)的圖象經過一、二、四象限的ai概率是 .
,使直線y=aix+i(i=1,2,…,2012)的圖象經過一、二、四象限的ai概率是 .
【答案】![]()
【解析】解:∵ai≠0(i=1,2,…,2012)滿足 ![]() ,∴(2012﹣1968)÷2=22,2012﹣22=1990,
,∴(2012﹣1968)÷2=22,2012﹣22=1990,
∴ai有22個是負數,1990個是正數,
∵ai<0時直線y=aix+i(i=1,2,…,2012)的圖象經過一、二、四象限,
∴使直線y=aix+i(i=1,2,…,2012)的圖象經過一、二、四象限的ai概率是 ![]() =
= ![]() ,
,
所以答案是: ![]() ,
,
【考點精析】關于本題考查的絕對值和概率公式,需要了解正數的絕對值是其本身,0的絕對值是0,負數的絕對值是它的相反數;注意:絕對值的意義是數軸上表示某數的點離開原點的距離;一般地,如果在一次試驗中,有n種可能的結果,并且它們發生的可能性都相等,事件A包含其中的m中結果,那么事件A發生的概率為P(A)=m/n才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】給出定義:設一條直線與一條拋物線只有一個公共點,且這條直線與這條拋物線的對稱軸不平行,就稱直線與拋物線相切,這條直線是拋物線的切線.有下列命題: ①直線y=0是拋物線y= ![]() x2的切線;
x2的切線;
②直線x=﹣2與拋物線y= ![]() x2 相切于點(﹣2,1);
x2 相切于點(﹣2,1);
③若直線y=x+b與拋物線y= ![]() x2相切,則相切于點(2,1);
x2相切,則相切于點(2,1);
④若直線y=kx﹣2與拋物線y= ![]() x2相切,則實數k=
x2相切,則實數k= ![]() .
.
其中正確命題的是( )
A.①②④
B.①③
C.②③
D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的中線BE,CF相交于點G,P、Q分別是BG、CG的中點.
(1)求證:四邊形EFPQ是平行四邊形;
(2)請直接寫出BG與GE的數量關系.(不要求證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】花粉的質量很小,一粒某種植物花粉的質量約為0.000037毫克,已知1克=1000毫克,那么0.000000037毫克可用科學記數法表示為( )
A.3.7×10﹣5克B.3.7×10﹣6克C.37×10﹣7克D.3.7×10﹣8克
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為64,E、F、G分別為AB、AC、BC的中點,A′、B′、C′分別為EF、EG、GF的中點,△A′B′C′的周長為_________.如果△ABC、△EFG、△A′B′C′分別為第1個、第2個、第3個三角形,按照上述方法繼續作三角形,那么第n個三角形的周長是__________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC為等邊三角形,點D為直線BC上的一動點(點D不與B、C重合),以AD為邊作菱形ADEF(A、D、E、F按逆時針排列),使∠DAF=60°,連接CF.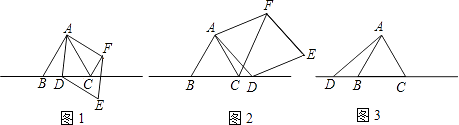
(1)如圖1,當點D在邊BC上時,求證:①BD=CF;②AC=CF+CD;
(2)如圖2,當點D在邊BC的延長線上且其他條件不變時,結論AC=CF+CD是否成立?若不成立,請寫出AC、CF、CD之間存在的數量關系,并說明理由;
(3)如圖3,當點D在邊CB的延長線上且其他條件不變時,補全圖形,并直接寫出AC、CF、CD之間存在的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是等腰直角△ABC外一點,把BP繞點B順時針旋轉90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,則P′A:PB=( ) 
A.1: ![]()
B.1:2
C.![]() :2
:2
D.1: ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com