
【題目】如圖,MN表示某引水工程的一段設計路線,從點M到點N的走向為北偏西30°,在點M的北偏西60°方向上有一點A,以點A為圓心,以500米為半徑的圓形區域為居民區,取MN上另一點B,測得BA的方向為北偏西75°.已知MB=400米,若不改變方向,則輸水路線是否會穿過居民區?請通過計算說明理由.(參考數據: ![]() ≈1.732)
≈1.732)

 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AE平分∠BAC交BC于點E,O是AB上一點,經過A,E兩點的⊙O交AB于點D,連接DE,作∠DEA的平分線EF交⊙O于點F,連接AF.
(1)求證:BC是⊙O的切線;
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求線段AC的長.
,求線段AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,四邊形BDEF是菱形,其中線段DF的長與DB相等,將菱形BDEF繞點B按順時針方向旋轉,甲、乙兩位同學發現在此旋轉過程中,有如下結論.
甲:線段AF與線段CD的長度總相等;
乙:直線AF和直線CD所夾的銳角的度數不變.
那么,你認為( )

A. 甲、乙都對 B. 乙對甲不對 C. 甲對乙不對 D. 甲、乙都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,點D為AB的中點.
(1)如果點P在線段BC上以1cm/s的速度由點B向點C運動,同時,點Q在線段CA上由點C向點A運動.當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
(2)若點Q以1.5cm/s的運動速度從點C出發,點P以原來的運動速度從點B同時出發,都逆時針沿△ABC三邊運動,則經過_____秒后,點P與點Q第一次在△ABC的AC邊上相遇?(在橫線上直接寫出答案,不必書寫解題過程)

查看答案和解析>>
科目:初中數學 來源: 題型:
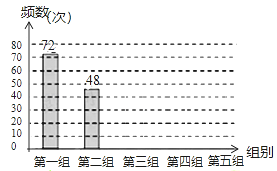
【題目】某網絡約車公司近期推出了”520專享”服務計劃,即要求公司員工做到“5星級服務、2分鐘響應、0客戶投訴”,為進一步提升服務品質,公司監管部門決定了解“單次營運里程”的分布情況.老王收集了本公司的5000個“單次營運里程”數據,這些里程數據均不超過25(公里),他從中隨機抽取了200個數據作為一個樣本,整理、統計結果如下表,并繪制了不完整的頻數分布直方圖(如圖).
組別 | 單次營運里程“x“(公里) | 頻數 |
第一組 | 0<x≤5 | 72 |
第二組 | 5<x≤10 | a |
第三組 | 10<x≤15 | 26 |
第四組 | 15<x≤20 | 24 |
第五組 | 20<x≤25 | 30 |
根據統計表、圖提供的信息,解答下面的問題:
(1)①表中a= ;②樣本中“單次營運里程”不超過15公里的頻率為 ;③請把頻數分布直方圖補充完整;
(2)請估計該公司這5000個“單次營運里程”超過20公里的次數;
(3)為緩解城市交通壓力,維護交通秩序,來自某市區的4名網約車司機(3男1女)成立了“交通秩序維護”志愿小分隊,若從該小分隊中任意抽取兩名司機在某一路口維護交通秩序,請用列舉法(畫樹狀圖或列表)求出恰好抽到“一男一女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料,回答問題:
解方程![]() ,這是一個一元四次方程,根據該方程的特點,它的解法通常是:
,這是一個一元四次方程,根據該方程的特點,它的解法通常是:
設![]() ,那么
,那么![]() ,于是原方程可變為
,于是原方程可變為![]() ①,解得
①,解得![]() ,
,![]() .
.
當![]() 時,
時,![]() ,∴
,∴![]() ;
;
當![]() 時,
時,![]() ,∴
,∴![]() ;
;
∴原方程有四個根:![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 在由原方程得到方程①的過程中,利用________法達到________的目的,體現了數學的轉化思想.
在由原方程得到方程①的過程中,利用________法達到________的目的,體現了數學的轉化思想.
![]() 解方程
解方程![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,則BC的長度為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一幅三角板的直角頂點重合放置,其中∠A=30°,∠CDE=45°.若三角板ACB的位置保持不動,將三角板DCE繞其直角頂點C順時針旋轉一周.若△DCE其中一邊與AB平行,則∠ECB的度數為____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com