
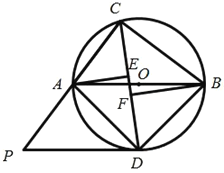
【題目】如圖,ABC內接于⊙O,AB為⊙O的直徑,∠ACB的平分線CD交⊙O于點D,過點D作⊙O的切線PD,交CA的延長線于點P,過點A作AE⊥CD于點E,過點B作BF⊥CD于點F.
(1)求證:PD//AB;
(2)求證:DE=BF;
(3)若AC=6,tan∠CAB=![]() ,求線段PC的長.
,求線段PC的長.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)連結OD,由AB為⊙O的直徑,根據圓周角定理得AB為⊙O的直徑得∠ACB=90°,再由ACD=∠BCD=45°,則∠DAB=∠ABD=45°,所以△DAB為等腰直角三角形,所以DO⊥AB,根據切線的性質得OD⊥PD,于是可得到DP∥AB;
(2)利用角的關系得出∠FBD=∠EDA,進而得出△FBD≌△EDA,即可得出DE=BF;
(3)在Rt△ACB中,利用AC=6,tan∠CAB=![]() ,可得BC=8,再利用勾股定理得出AB=10,由△DAB為等腰直角三角形,可得AD=5
,可得BC=8,再利用勾股定理得出AB=10,由△DAB為等腰直角三角形,可得AD=5![]() ,由AE⊥CD,得出△ACE為等腰直角三角形,得出AE=CE=3
,由AE⊥CD,得出△ACE為等腰直角三角形,得出AE=CE=3![]() ,在Rt△AED中,可得DE=4
,在Rt△AED中,可得DE=4![]() ,得出CD=7
,得出CD=7![]() ,由角的關系得出△PDA∽△PCD,利用比例式可得出PA=
,由角的關系得出△PDA∽△PCD,利用比例式可得出PA=![]() PD,PC=
PD,PC=![]() PD,由PC=PA+AC,可求得PD=
PD,由PC=PA+AC,可求得PD=![]() ,即可得出PC的值.
,即可得出PC的值.
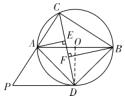
證明:(1)連結![]() ,如圖,
,如圖,
∵![]() 為
為![]() 的直徑,∴
的直徑,∴![]() ,
,
∵![]() 的平分線交
的平分線交![]() 于點
于點![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∵![]() 為
為![]() 的切線,∴
的切線,∴![]() ,∴
,∴![]() .
.
(2)∵![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
(3)在![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
∵![]() ,
,
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某校為了解九年級學生新冠疫情防控期間每天居家體育活動的時間(單位:![]() ),在網上隨機調查了該校九年級部分學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
),在網上隨機調查了該校九年級部分學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
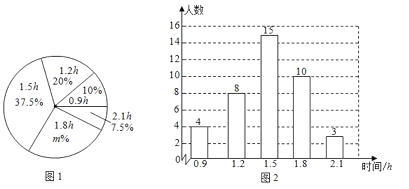
(1)本次接受調查的初中學生人數為________,圖①中![]() 的值為________;
的值為________;
(2)這組數據的平均數是________,眾數是________,中位數是________;
(3)根據統計的這組每天居家體育活動時間的樣本數據,估計該校500名九年級學生居家期間每天體育活動時間大于![]() 的學生人數.
的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,AB為⊙O的直徑,D為![]() 的中點,過D作DF⊥AB于點E,交⊙O于點F,交弦BC于點G,連接CD,BF.
的中點,過D作DF⊥AB于點E,交⊙O于點F,交弦BC于點G,連接CD,BF.
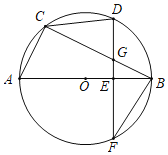
(1)求證:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的長;
(3)在(2)的條件下,P為⊙O上一點,連接BP,CP,弦CP交直徑AB于點H,若△BPH與△CPB相似,求CP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖1,四邊形![]() 是正方形,
是正方形,![]() 分別在邊
分別在邊![]() 、
、![]() 上,且
上,且![]() ,我們把這種模型稱為“半角模型”,在解決“半角模型”問題時,旋轉是一種常用的方法.
,我們把這種模型稱為“半角模型”,在解決“半角模型”問題時,旋轉是一種常用的方法.
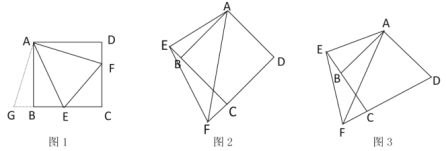
(1)在圖l中,連接![]() ,為了證明結論“
,為了證明結論“![]() ”,小亮將
”,小亮將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后解答了這個問題,請按小亮的思路寫出證明過程;
后解答了這個問題,請按小亮的思路寫出證明過程;
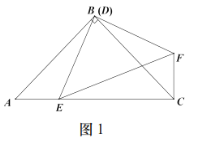
(2)如圖2,當![]() 繞點
繞點![]() 旋轉到圖2位置時,試探究
旋轉到圖2位置時,試探究![]() 與
與![]() 、
、![]() 之間有怎樣的數量關系?
之間有怎樣的數量關系?
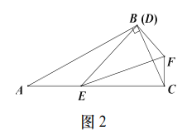
(3)如圖3,如果四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 中
中![]() 點
點![]() 分別在邊
分別在邊![]() 、邊
、邊![]() 上,連接
上,連接![]() 點
點![]() 、點
、點![]() 在直線
在直線![]() 同側,連接
同側,連接![]() 且
且![]() .
.
(1)點![]() 與點
與點![]() 重合時,
重合時,
①如圖1,![]() 時,
時,![]() 和
和![]() 的數量關系是 ;位置關系是 ;
的數量關系是 ;位置關系是 ;
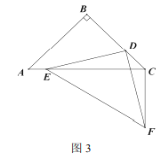
②如圖2,![]() 時,猜想
時,猜想![]() 和
和![]() 的關系,并說明理由;
的關系,并說明理由;
(2)![]() 時,
時,
③如圖3,![]() 時,若
時,若![]() 求
求![]() 的長度;
的長度;
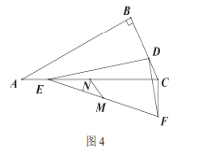
④如圖4,![]() 時,點
時,點![]() 分別為
分別為![]() 和
和![]() 的中點,若
的中點,若![]() ,直接寫出
,直接寫出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售部有營業員20人,該公司為了調動營業員的積極性,決定實行目標管理,根據目標完成的情況對營業員進行適當的獎勵,為了確定一個適當的月銷售目標,公司有關部門統計了這20人某月的銷售量,如下表所示:
某公司20位營業員月銷售目標統計表
月銷售量/件數 | 1760 | 480 | 220 | 180 | 120 | 90 |
人數 | 1 | 1 | 3 | 5 | 6 | 4 |
請根據以上提供的信息解答下列問題:
(1)求這個月中20位營業員的月銷售量的平均數;
(2)為了提高大多數營業員積極性,公司將發放A,B,C三個等級的獎金(金額:![]() ),如果你是管理者,從平均數,中位數,眾數的角度進行分析,你將如何確定領取A,B,C級獎金各需達到的月銷售量.
),如果你是管理者,從平均數,中位數,眾數的角度進行分析,你將如何確定領取A,B,C級獎金各需達到的月銷售量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠BAC=30°,把△ABC繞著點A順時針旋轉到△ADE的位置,使得點D,A,C在同一直線上.
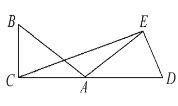
(1)△ABC旋轉了多少度?
(2)連接CE,試判斷△AEC的形狀;
(3)求 ∠AEC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
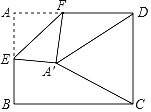
【題目】如圖,在矩形紙片ABCD中,AB=4,BC=4![]() ,點E是AB的中點,點F是AD邊上的一個動點,將△AEF沿EF所在直線翻折,得到△A'EF,連接A'C,A'D,則當△A'DC是以A'D為腰的等腰三角形時,FD的長是_____.
,點E是AB的中點,點F是AD邊上的一個動點,將△AEF沿EF所在直線翻折,得到△A'EF,連接A'C,A'D,則當△A'DC是以A'D為腰的等腰三角形時,FD的長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網店專售一款電動牙刷,其成本為20元/支,銷售中發現,該商品每天的銷售量y(支)與銷售單價x(元/支)之間存在如圖所示的關系.
(1)求y與x之間的函數關系式.
(2)由于湖北省武漢市爆發了新型冠狀病毒肺炎(簡稱“新冠肺炎”)疫情,該網店店主決定從每天獲得的利潤中抽出200元捐獻給武漢,為了保證捐款后每天剩余利潤不低于550元,如何確定這款電動牙刷的銷售單價?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com